・目次追加
・冒頭部に見出し「概要」追加
・誤記修正(ランベルトのW関数の式の表記)
誤:\(\displaystyle w=L[x]\)
正:\(\displaystyle w=W[x]\)
・プログラムのソースのコメント変更
変更前:Iterate to find Lambert's W
変更後:Lambert W関数の計算処理
・プログラムソースの補足説明の追加
追加内容:PC側でa=0.099999999…や0.100000001…といったような値で解釈されてしまう、ということです。
(「後日追加予定」の表記削除)
カワッターです。
久々のVBAの投稿です。
今回はHalley法を用いたランベルトのW関数のVBAソースをアップしました。
eのべき乗の逆関数を求めたい方の助けになればと思います。
概要
ランベルトのW関数はeのべき乗の逆関数を求めるために使用します。
具体的には次の方程式の関係の場合に使用できます。
\(\displaystyle x=we^{w}\)
これの逆関数を
\(\displaystyle w=W[x]\)
とすることができ、\(W[x]\)がランベルトのW関数となります。
今回は\(W[x]\)の計算部分をVBAで実装しています。
変数wは複素数です。
ただ今回は実部のみに注目しているため、複素領域\(i\)の部分は出てきません。
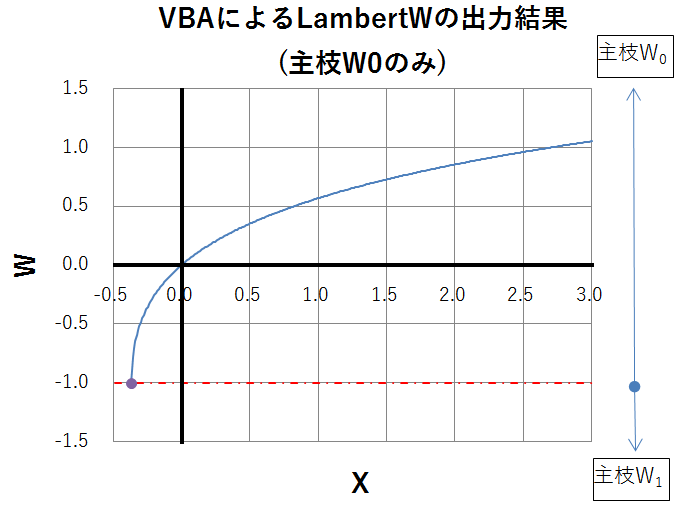
この条件の場合、計算する領域は主枝\(\displaystyle W_{0}\)となります。
主枝\(\displaystyle W_{0}\)の範囲はwの値が-1以上です。
グラフのイメージは冒頭のサムネを参照ください。
より詳しい説明は参考文献の章にあるWikipediaのページを参照ください。
ランベルトのW関数は次の記事にあるLTspiceのソーラーパネルの温度特性を再現するためのパラメータを求めるときの副産物としてできました(今はパラメータ計算に使用していません)。
また、まだ予定の段階ですが、作品集のページに標準モジュールとxlsm形式のファイルをアップするつもりです。
→アップしました。
LTspiceのソーラーパネルの温度特性を再現の記事です。
作品集のページにVBAの標準モジュールファイルをアップしています。
ソースは本記事を参照ください。
プログラムソース
使用イメージ図を参照ください。
標準モジュールを作成後、ソースをコピペして使用ください。
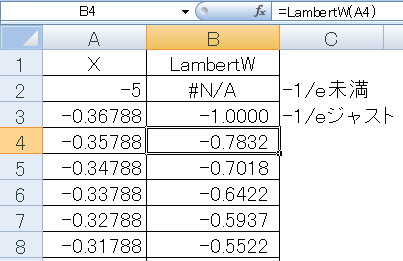
登録後セルで「=LambertW(セルを指定)」とすれば値が返ります。
'''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
' LambertW function (W0領域のみ)
'
' 機能:引数に入力された値のLambertWの値を返す
' Halley法を使用
'
' 引数:inputX...LambertW関数のX軸の値
'
' 返り値:
' 0...inputXが0の場合
' -1...inputXが-1/e±1p(ピコ)以内の場合
' N/A...inputXが-1/e-1p(ピコ)未満の場合
' W...Halley法の出力結果
'
'参考ソース:https://blogs.mathworks.com/cleve/2013/09/02/the-lambert-w-function/
'
Option Explicit
Public Function LambertW(inputX As Double)
'W0領域境界条件用(X=-1/eの時の判定用)
Dim thresholdValue As Double: thresholdValue = (-1 / Exp(1))
Dim errValue_ForThreshold_W0 As Double: errValue_ForThreshold_W0 = 1 * 10 ^ (-12) '許容誤差(1p-ピコ)
'Halley法計算用
Dim W As Double
Dim tmpE As Double
Dim tmpFw As Double
Dim tmpW As Double
Dim iCount As Long
Dim isFound As Boolean
Dim errValue_ForThreshold_Halley As Double: errValue_ForThreshold_Halley = 1 * 10 ^ (-12) '許容誤差(1p-ピコ)
If inputX = 0 Then '0が入力されたら0を返す
LambertW = 0
ElseIf Abs(inputX - thresholdValue) <= errValue_ForThreshold_W0 Then 'inputXが1/e±1p以内であれば-1を返す
LambertW = -1
ElseIf inputX < (thresholdValue - errValue_ForThreshold_W0) Then 'inputXが(1/e-1p)未満であればエラーN/A(値見つからず)を返す
LambertW = CVErr(xlErrNA)
Else
isFound = False ' 収束フラグ設定
W = 1 '初期値を決定(参考ソースを読み解くと1を代入している)
' Lambert W関数の計算処理
For iCount = 1 To 300
'Halley法
tmpE = Exp(W)
tmpFw = W * tmpE - inputX
tmpW = W - tmpFw / ((tmpE * (W + 1) - tmpFw * (W + 2) / (2 * W + 2)))
'誤差の範囲内なら収束フラグをTrue
If ((Abs(W - tmpW) < errValue_ForThreshold_Halley)) Then
isFound = True
Exit For
Else
W = tmpW '計算した値を一時保存
End If
Next iCount
Debug.Assert (isFound) '自分通知用 他の方に使って頂くときなどはコメントアウト
'返り値決定
LambertW = W
End If
End Function
関数の型は宣言していません。
関数の返り値にエラー関数CVErr()の値を含めたかったからです。
今回のプログラムでは文字列の場合のエラー処理はいれていません。
そのため引数に文字列で指定しないでください、エラーになります。
必要な場合、分岐処理を適宜追加してください。
引数に入力するinputXの値が-1/eのとき-1になりますが、このとき領域\(W_{0}\)と\(W_{1}\)の閾値となるためプログラムは収束しません。
そのため1/e±1pの範囲内で-1を返すようにしています。
±1pの範囲で判定した理由は次の2点です。
- ifの判定にdouble型を使用しているから
double型は浮動小数(2進数による小数点の表現)なので、
数値同士の計算後、こちらの意図した値が入っていない可能性があります。
つまりどーゆーことやねん、というと定義の段階で人間側でdouble a=0.1と明示しても、PC側でa=0.099999999…や0.100000001…といったような値で解釈されてしまう、ということです。 - LTspiceのソーラーパネルの温度特性のパラメータを計算する目的であれば1pの範囲で十分足りるから
型による演算の誤差の扱いは細かいくらいに気を使う必要があります。
詳細はquitaのQ11Q様の記事リンクをつけましたので、参照ください。

計算が収束したかどうかをはっきりと確認したかったため、収束フラグisFoundにDubug.Assertをつかっています。
Dubug.Assertの説明はこちらの記事が詳しいです。
是非一読ください。
(えくせるちゅんちゅん様の記事です)
Dubug.Assertを使った理由は音が鳴る&VBEが自動で起動するからです。
私はずぼらなので、収束しなかった場合に音がならないと気づかない&何かあったらエディタが立ち上がって欲しいなぁとおもっていました。
記事にも書いてありますが、自分以外の方に使ってもらう場合はDubug.Assertをコメントアウトするなどして無効にした方が良いです。
原理(参考文献)
ランベルトのW関数の原理(参照文献)は次のページを参考にしました。
原理式からVBAにおとし仕込んでいます。
全体を見渡したい参考(Wikipedia)

VBA作成時の参考(Mathworks-MATLABソース)
MathworksのHPです。
MATLABのソース(mファイル)があります。
今回はMATLABのソースからVBAに書き直しています。
MATLABのソースは主枝\(W_{1}\)の計算も含めています。
私の場合はLTspiceのパラメータ算出に複素数を使いませんでしたので、主枝\(W_{0}\)のみの領域のみの再現に絞っています。
というのは体の良い言い訳で、正直なところ、まだMATLABソースの主枝\(W_{1}\)に関するソースを読み解けていないです。
余談ですが大学の時はMathmatica、大変お世話になりました。
アームロボットの速度制御のために逆ヤコビアンを求めるときに使っていました。
文字の行列計算が計算過程を含めパパッとされる衝撃は今でも忘れられません。
(ちなみにもう逆ヤコビについては何も思い出せません)





コメント スパム対応をしたつもり、コメントは残す方向で頑張ってます