LTspice向けソーラーパネルのシミュレーションモデルで温度特性を再現できました。
変数{T}に温度(セ氏:℃)を指定後、シミュレーションGOします。
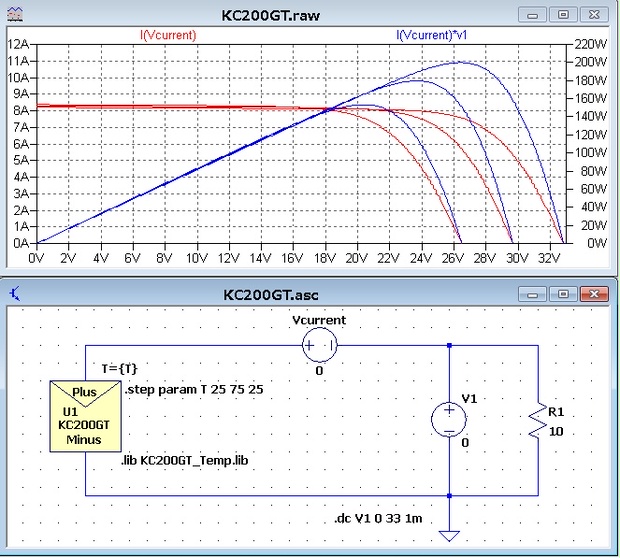
サムネイルのように.step文で複数パターン可能です。
サムネイルはDC解析をした時のものです。
有償で本記事の内容のソーラーパネルモデル製作しています。
ご依頼ありましたらページ最後のリンクにて。
要約
ライブラリファイルはこちらです。
既にアップしているお試し版モデルの京セラ製KC200GTのバージョンをアップしました。
結果をTwitterにアップしています。
KC200GT以外にGWソーラー製のGW-E115Aをあわせて再現しました。
また、この記事を作成した段階ではLTspice用のGW-E115Aライブラリファイルを製作していません。
GW-E115Aの方の引用リツイートで当時のRsの算出案がありますが無視してください。
後の章で図を変えて説明しています。
京セラ製KC200GT
GWソーラー製
【データシート】
京セラ製KC200GTのデータシートは本家HPを探してもありませんでした。
GWソーラー製GW-E115Aは本家HPに基本特性はありましたが温度特性がなしでした。
なので代わりのページを探しました。
京セラ製KC200GTデーターシート(pdf直リンクです)。
GWソーラー製GW-E115Aデータシート(Download Datasheetをクリックしてください)
今後は色々なソーラーパネルの温度特性の再現モデルを販売していく予定です。
この記事をアップしている段階では25℃対応(STC条件)のモデルのみ販売しています。
サムネイルは京セラ製ソーラーパネルKC200GTのシミュレーション結果です。
KC200GTはソーラーパネルのパラメータを算出するための論文でよく見かけるように思います。
ノウハウがあるため販売時にはライブラリファイルを暗号化しています。
上記のお試し版も同様です。
ただ、ライブラリファイルを暗号化すると動作がブラックボックス化されるため、内部の動作が分からなくなります。
内部の動作が分からないということは、モデルの正当性の検証ができなくなってしまうことと同義です。
ユーザから見ればどういった原理で動いているのか分からないモデルを使っていることになります。
そこで本ブログで温度特性を再現するために使用した原理をまとめることとしました。
本来メーカーの場合だと今回のような内容は社外秘にすることが大半です。
しかしながら、私は電子回路シミュレーションの地位向上のために、原理を公開することは意義があることだと考えています。
また、私の製作したモデルの質の検証確認に使用頂ければと思います。
LTspiceパラメータはメーカのソーラーパネルのデータシートのパラメータから求めています。
Energiesの論文の手法がメインです。
そこから他の引用ページ・論文で内容を補完しています。
引用した参考文献
Energies論文
以後、参考文献[1]とします
A New Simplified Five-Parameter Estimation Method for Single-Diode Model of Photovoltaic Panels, November 2019 Energies 12(22):4271
飽和電流Isの温度特性
以後、参考文献[2]とします
ダイオードのモデリング 式(1.4) 金沢大学 Akio Kitagawa
ダイオード指数Nの温度特性
以後、参考文献[3]とします
Relationship Between the Diode Ideality Factor and the Carrier Recombination Resistance in Organic Solar Cells, September 2018IEEE Journal of Photovoltaics 8(6):1701 - 1709
参考文献[3]の式(11)に項を追加してNを算出しています。
上記の論文・ページを引用した理由は以下の通りです。
- ソーラーパネルメーカのデーターシートをもとにしたLTspiceの基準パラメータと温度変更時の原理式、両方に適用できた。
- パラメータの算出方法の考え方が非常にシンプルかつ簡便にまとまっていた
- 計算プログラムが一緒に公開されていた
論文の計算プログラムのソースコードはMATLAB用であったため、今回私がVBA用にしています - この記事を作成している現段階で情報は無償で公開されており、誰でも閲覧可能であった
(情報がオープンであることは技術の発展において重要)
ただし、基準パラメータを算出するプログラムのソースコードに微妙な間違いがあるため、入念に内容チェックが必要です(カッコのとじ位置関係がおかしいなど)。
また、任意のひとつの温度のみの対応になりますが、これから私のモデルを購入頂く方もこの記事の内容で25℃対応モデルから任意温度のモデルに変更可能です。
上記より論文・ページの内容を理解できれば私が販売しているモデルを購入頂く必要はないと考えています。
少しでも余計なお金を支払い頂く必要はないと考えていますので、ぜひ実施してみてください。
私が販売しているモデルと同レベルのものができるはずです。
温度特性のシミュレーションの説明
概要(温度変更前の基準パラメータの求め方について)
内容の説明の前に、ソーラーパネルの物性式をLTspiceのパラメータと対応させた内容で示します。
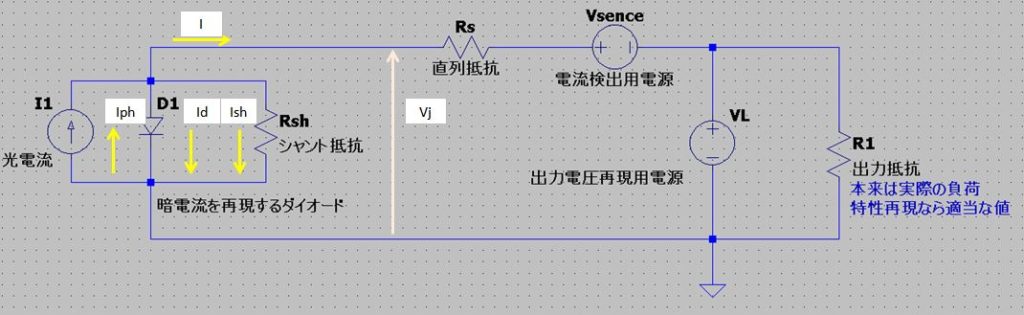
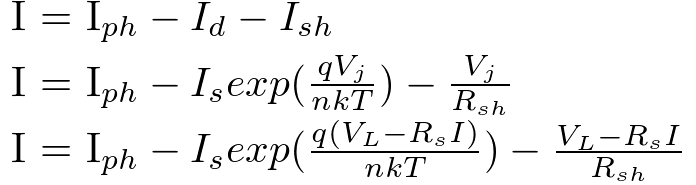

パラメータの求め方は以下の通りです。
それぞれの求め方step1・step2と大別されます。
- step1:このstepで求めたLTspice用のソーラーパネル用パラメータのことを「基準パラメータ」とします。
基準パラメータはソーラーパネルメーカのデータシートの物性値からを算出します。
参考文献[1]の原理式をもとに計算プログラムを作成、繰り返し計算させて求めます。 - step2:求めた基準パラメータから参考文献[1]・参考文献[2]・参考文献[3]で任意温度時のLTspiceパラメータを再計算します。
上記の式とstepをまとめ、求めるパラメータは次の表の内容となります。
| 記号 | パラメータ名 | step1(STC) 基準パラメータ | step2(任意温度) |
| Iph(Isc) | 光電流(短絡電流値) | 計算 | 再計算 |
| Is(I0) | (逆)飽和電流 | 計算 | 再計算 |
| N(N) | ダイオード指数 ソーラーパネルでは(n*セル数) nはダイオード素子1つ分の ダイオード指数(名称Ideality Factor) | 計算 | 再計算 |
| Rsh(Rp) | シャント抵抗 | 計算 | 計算せず step1の値をそのまま使用 |
| Rs(Rs) | 半導体バルク、オーミックコンタクトの 接触抵抗などを含めた直列抵抗 | 計算 | 再計算 |
今回と前回の記事の相違点(基準パラメータ計算方法)
今回説明する内容は前回の記事と比べてソーラーパネルの基準パラメータの求め方が異なります。
下記により、BOOTHで販売しているものと今回の温度特性対応モデルはデータシートで用いられるStandard Test Conditions(STC)の状態を基準としています。
STC:1000W/m2・AM1.5(太陽角度θ=41.8°)・温度 25℃
【今回の手法】
参考文献[1]~[3]のリンクを再掲
主な相違点は以下の通りです。
- Rsの値
今回:第2項と第3項のRs(掲載した式の赤文字と黒文字)の値は同じ
前回:第2項と第3項のRs(掲載した式の赤文字と黒文字)の値は異なる
物理的な解釈を別にしているため値が異なります。
第2項:ダイオードの内部抵抗
(パラメータとして使用、回路図には記載されていません)
第3項:直列抵抗 - パラメータ算出に用いるデータが異なる
今回:メーカのソーラーパネルのデータシートの値
前回:実測値(入射強度、太陽角度Θ、温度は実測時の値)
各パラメータの温度特性の再現式(原理式)
ここではstep1のLTspice用の基準パラメータの計算が完了したものとしています。
以後、温度について次の通りとします。
\(T0\):STC時の温度25℃(≒298K)
\(T1\):任意温度(≒(T1+273)K)
また、数式の乗算は記号のみやすさのためにアスタリスク"*"を付している箇所があります。
(カワッターの独断と偏見です)
Iph(Isc):短絡電流
参考文献[1]より温度変化時の短絡電流は次式の通りに変化します。
\(\displaystyle I_{ph(T1)} = I_{ph(T0)}*\frac{G}{G_{(T0)}}+K_{i}(T1-T0)\)
今回は日射強度は変更しないため\(\displaystyle \frac{G}{G_{(T0)}}=1\)
よって \(\displaystyle I_{ph(T1)} = I_{ph(T0)}+K_{i}(T1-T0)\)
\(\displaystyle I_{ph(T1)}\):温度T1の時の短絡電流
\(\displaystyle I_{ph(T0)}\):温度T0の時の短絡電流(step1の基準パラメータ)
\(\displaystyle G\):日射強度(この記事では\(\displaystyle G=G_{(T0)}\))
\(\displaystyle K_{i}\):1℃ごとの短絡電流変化率[A/℃または%/℃] ※データシートから求める
日射強度の項Gがありますが、今回は温度変化の影響のみを含めているため省略します。
つまり日射強度は今回の場合\(\displaystyle G=G_{(T0)}\)とし\(\displaystyle \frac{G}{G_{(T0)}}=1\)となります。
よって最終的な式は\(\displaystyle I_{ph(T1)} = I_{ph(T0)}+K_{i}(T1-T0)\)となります。
\(\displaystyle K_{i}\)はデータシートの\(\displaystyle I_{ph}\)の温度係数を参照します。
京セラ製KC200GTの場合、\(\displaystyle K_{i}\)は\(\displaystyle 3.18×10^{-3}\) A/℃と記載あります。
step1で\(\displaystyle I_{ph(T0)}\)が、\(\displaystyle T1\)=任意温度、\(\displaystyle T0\)=25℃で与えられるため、あとは計算式で\(\displaystyle I_{ph(T1)}\)を求めます。
Is(I0):(逆)飽和電流[saturation current]
参考文献[2]より、Isは下記の通りとなります。
\(\displaystyle Is_{(T1)}=Is_{(T0)}*(\frac{T1}{T0})^\frac{XTI}{n_{(T0)}}*e^{(\frac{-q*EG}{n_{(T0)}*k*T1})(1-\frac{T1}{T0})}\)
\(\displaystyle Is_{(T1)}\):温度T1の時の(逆)飽和電流[A]
\(\displaystyle Is_{(T0)}\):温度T0の時の(逆)飽和電流[A](step1の基準パラメータ)
\(\displaystyle XTI\):(逆)飽和電流の温度指数
[Saturation current temperature exponent]
XTI=3です。補足としてXTIは以下の条件で決定します。
| ダイオード種類 | 値 |
| ジャンクションダイオード(jn) | 3 |
| ショットキーバリアダイオード(sbd) | 2 |
引用:LTspice HELP LTspice XVII 1998-2018 Analog Devices Corporation
\(\displaystyle q\):電荷量 \(1.60218*10^{-19}\)[C]
\(\displaystyle k\):ボルツマン定数 \(1.38065*10^{-23}\)[J/K]
\(\displaystyle n_{(T0)}\):ダイオード素子1つ分のダイオード指数[Ideality Factor]
\(n_{(T0)}\)は次の2つの方法で求めることができます。
【step1から直接求める方法】
参考文献[1]より基本パラメータの計算過程(プログラムGO)で直接求めます。
【私が販売しているモデルから求める方法】
nはソーラーパネルのダイオード指数Nと次の関係をもっています。
\(\displaystyle N=n*セル数\)
上記式の関係を利用して、nを求めます。
nは\(T0\)の時の値を使用します。
よって、\(\displaystyle N_{(T0)}=n_{(T0)}*セル数\)となります。
上記2つの方法はどちらも”セル数”の把握が必要となります。
次のどちらかの方法で確認します。
- 方法1:ソーラーパネルのデータシートにある「セル数」を参照します。
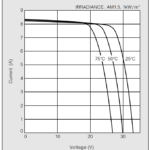
京セラ製KC200GTの場合、”Number per Module”にある54を適用します。 - 方法2:データシートに「セル数」の記載がない場合があります。
その場合は製品写真からセル数を予測します。
KC200GTの製品写真を確認すると、ちょうど9行×6列=54のセル数となっていることが確認できます。
他のソーラーパネルでも同じ要領で確認を行います。
私が販売しているモデルから求める方法で求めたnはstep1の値と全く同じにはなりません。
step1の方法はnを0.01単位で調整していますが、上記式は単純な除算ですので0.01より下の桁も出すからです。
\(\displaystyle EG\):活性化エネルギー[Activation energy][eV]
EG=1.11です。
京セラ製KC200GTのソーラーパネルは参考文献[1]よりシリコンダイオード製相当と分かります。
補足としてEGは以下の条件で決定します。
| 材料種類 | 値 |
| シリコンダイオード(Si) | 1.11 |
| ショットキーバリアダイオード(sbd) | 0.69 |
| ゲルマニウムダイオード(Ge) | 0.67 |
引用:LTspice HELP LTspice XVII 1998-2018 Analog Devices Corporation
N(N):ダイオード指数[Emission coefficient]
Nは下記の通りとなります。
参考文献[3]をもとにしていますが、参考文献[3]はソーラーパネルの物性式の第3項を無視しているため、私の方で再計算しています(参考文献[3]はRshを含めた式になっていません)。
\(\displaystyle N_{(T1)}=\frac{q*V_{oc(T1)}}{k*T1}*\frac{1}{ln(\frac{I_{ph(T1)}+\frac{V_{oc(T1)}}{R_{sh}}}{I_{s(T1)}}+1)}\)
\(\displaystyle N_{(T1)}\):温度T1の時のソーラーパネルのダイオード指数[単位無し]
\(\displaystyle N_{(T0)}\):温度T0の時のソーラーパネルのダイオード指数[単位無し]
\(\displaystyle V_{oc(T1)}\):温度T1の時の開放電圧[V]
\(\displaystyle V_{oc(T1)}\)は参考文献[1]より以下の式で求まります。
\(\displaystyle V_{oc(T1)}=V_{oc(T0)}+K_{v}(T1-T0)+v_{t(T1)}ln(\frac{G}{G_{(T0)}})\)
ただし、日射強度の第3項はまだ検証できていません。
今回は日射強度は変更しないため\(\displaystyle \frac{G}{G_{(T0)}}=1\)
よって \(\displaystyle V_{oc(T1)}=V_{oc(T0)}+K_{v}(T1-T0)\)
\(\displaystyle V_{oc(T0)}\):温度T0の時の開放電圧[V] ※データシートから求める
\(\displaystyle K_{v}\):1℃ごとの開放電圧変化率[V/℃または%/℃] ※データシートから求める
\(\displaystyle v_{t(T1)}\):温度T1の時の熱起電力[V] ※この記事では未検証
\(\displaystyle G\):日射強度 ※この記事では\(\displaystyle G=G_{(T0)}\)
\(\displaystyle I_{ph(T1)}\):温度T1の時の短絡電流 ※前節Iphを計算する時に求める
\(\displaystyle R_{sh}\):シャント抵抗(step1の基準パラメータ)
\(\displaystyle I_{s(T1)}\):温度T1の時の(逆)飽和電流[A] ※前節Isを計算する時に求める
Rs(Rs):半導体バルク、オーミックコンタクトの接触抵抗などを含めた直列抵抗[Ohmic resistance]
参考文献[1]よりRsは下記の通りとなります。
\(\displaystyle R_{s(T1)}=\frac{V_{oc(T1)}}{I_{mp(T1)}}+\frac{V_{t(T1)}}{I_{mp(T1)}}ln(\frac{V_{t(T1)}}{V_{t(T1)}+V_{mp(T1)}})-\frac{V_{mp(T1)}}{I_{mp(T1)}}\)
\(\displaystyle R_{s(T1)}\):温度T1の時の直列抵抗[Ω]
\(\displaystyle V_{oc(T1)}\):温度T1の時の開放電圧[V] ※前節Nを計算する時に求める
\(\displaystyle I_{mp(T1)}\):温度T1の時の最大出力動作電流[A]
\(\displaystyle V_{t(T1)}\):温度T1の時の熱起電力[V]
\(\displaystyle V_{t(T1)}\)は参考文献[1]より以下の式で求まります。
\(\displaystyle V_{t(T1)}=\frac{k*T1*n_{(T1)}*セル数}{q}=\frac{k*T1*N_{(T1)}}{q}\)
\(\displaystyle k\):ボルツマン定数 \(1.38065*10^{-23}\)[J/K]
\(\displaystyle N_{(T1)}\):ソーラーパネルのダイオード指数 ※前節\(N_{(T1)}\)を計算する時に求める
また、\(N_{(T1)}=n_{(T1)}*セル数\)
\(\displaystyle q\):電荷量 \(1.60218*10^{-19}\)[C]
\(\displaystyle V_{mp(T1)}\):温度T1の時の最大出力動作電圧[V]
\(\displaystyle I_{mp(T1)}\)と\(\displaystyle V_{mp(T1)}\)はメーカのデータシートに温度ごとの電流波形グラフの有無で求め方が異なります。
メーカのデータシートに温度ごとの電流波形グラフがある場合
ソーラーパネルメーカのデータシートに記載してある温度ごとの波形から直接値をプロットします。
ただ、データーシートの波形グラフのプロットを目視でやろうとすると非常にざっくりとした値しかプロットできない場合がほとんどです。
そこで次のサイトのツールを使用します。
画像データのグラフからX軸・Y軸の起点値と終点値を与えて欲しい点をクリックしていくと自動で値をとってくれます。
あとは取り出したデータから\(\displaystyle I_{mp(T1)}\)と\(\displaystyle V_{mp(T1)}\)を探して\(\displaystyle R_{s(T1)}\)の式に当てはめていきます。
百聞は一見にしかず。ぜひやってみてください。
メーカのデータシートに温度ごとの電流波形グラフがない場合
T1時のフィルファクターを元にしたVmpを変化させたときの最大動作電流Impが、最大動作電力Pmaxになるようなポイントを求めます。
もう少し掘り下げて説明します。
使用するのは次の式です。
\(\displaystyle I_{mp(T1)}=F\frac{V_{oc(T1)}I_{ph(T1)}}{V_{mp(T1)}}\)
\(F=\frac{P_{max(T1)}}{V_{oc(T1)}I_{ph(T1)}}\):フィルファクター(細かい説明です(電光石科様))
\(P_{max(T1)}=P_{max(T0)}+P_{x}(T1-T0)\)
\(P_{x}\):電力係数[W/℃]または[%/℃]…データシートから求める
【2021/5/31】
申し訳ありません、\(P_{max(T1)}\)の2項目の符号を間違えました。
"-"から"+"に変えています。
\(\displaystyle \frac{dP_{(T1)}}{dV}=\)
\(I_{ph(T1)}-I_{s(T1)}[e^{\frac{V_{mp(T1)}+R_{s(T1)}*I_{mp(T1)}}{V_{t(T1)}}}-1]\)
\(+V_{mp(T1)}[-\frac{I_{s(T1)}}{V_{t(T1)}}e^{\frac{V_{mp(T1)}+R_{s(T1)}*I_{mp(T1)}}{V_{t(T1)}}}]=0\)
参考文献[1]より
\(R_{s(T1)}=R_{s(T0)}+K_{Rs}(T1-T0)\)
\(K_{Rs}\):1℃ごとの抵抗変化率
変化させる数値は\(V_{mp(T1)}\),\(K_{Rs}\)です。
また、\(V_{mp(T1)}\)を変化させると一つ目の式より\(I_{mp(T1)}\)も変化していきます。
このとき、\(\frac{dP_{(T1)}}{dV}=0\)を満たすような\(V_{mp(T1)}\),\(I_{mp(T1)}\),\(K_{Rs}\)を求めていきます。
\(K_{Rs}\)を変化させてもとめた\(R_{s(T1)}\)とこの節の冒頭で示した参考文献[1]の\(R_{s(T1)}\)の値が相当に近くなることを確認します。
ここで、一気に3つの変数を変化させて\(\frac{dP_{(T1)}}{dV}=0\)とさせる訳ですから、人間の手作業では無茶です。
そのため例のごとくEXCELのソルバー機能を用います。
ソルバー機能を使う前の段取りが非常に大変ですが、是非とも頑張ってやってみてください!
上記の式から見て分かると思いますが、Rs以外のパラメータはT1の状態です。
つまり、全て計算済みである必要があります。
Rsの式を記事の最後にもってきたのはこのためです。
検証結果
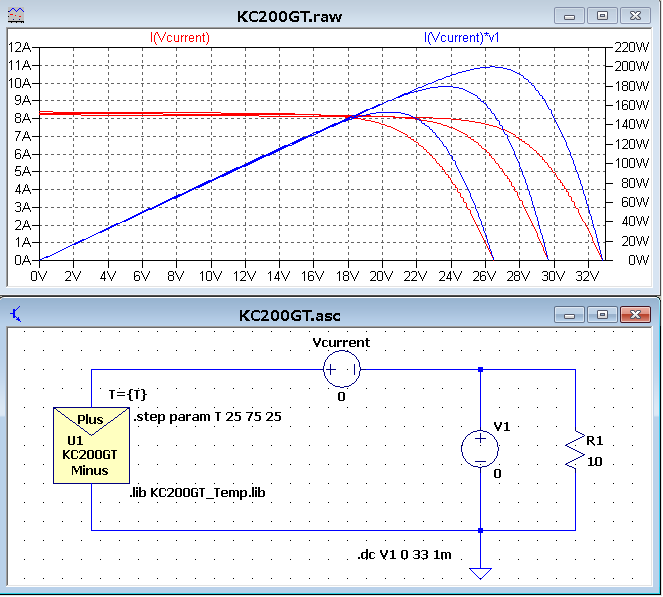
京セラ製KC200GTとGWソーラー製GW-E115Aのソーラーパネルの温度特性の結果を再掲します。
冒頭のTwitterでアップしていた画像と同じものです。
計算過程はstep1・step2の手順で求めています。
そのためダイオード1つ分のダイオード指数nの有効桁数は小数点第2です(0.01刻み)。
Twitterにアップした内容は冒頭のパラメトリック解析ができるようになる前のものです。
この結果より、私のモデルを購入頂く方はこの記事の内容で25℃対応モデルから任意温度のモデルに変更可能ということが確認できます。
ただし、私のライブラリファイルからnを求めると小数点第3以下も数値としてでるため、厳密にまったく同じ結果となるわけではありません。
本記事のソーラーパネルモデル製作します(有償)
今回の内容のソーラーパネルモデルの製作依頼ありましたら下記リンクにて。
【必要パラメータ】
・STC特性:Pmax・Vmpp・Impp・Voc・Isc
・温度特性:STC特性に加えVoc・Isc・Pの温度変化率
【2022/2/6】個人運営により管理が追い付かないため、現在更新をストップしています。
今後は色々なパネルの温度特性を再現・販売していく予定です。
この記事をアップしている段階では25℃のモデルのみ販売しています。
→BOOTHのリンクをアップしました。
変更履歴
文言修正
(大きな表示の広告は内容の連続性を弱めるため)
細部の文章構成を若干変更。
②冒頭部下記変更
・章「要約」として章だて(前置きと言うには長いため)
・本ブログ簡易版(Twitter)を追加
・文言微修正
誤:1-T2/T1
正:1-T1/T0








コメント スパム対応をしたつもり、コメントは残す方向で頑張ってます