”5.2”節の画像サイズ修正、各部の誤字脱字修正、リンク表記修正
はじめに、この記事は@EN_gelou様(Twitter)が測定頂いたデータを使用させて頂いております。
この場を借りてお礼申し上げます。
誠にありがとうございました。
【2021/5/20】ソーラーパネルの温度特性を再現できました。
要約
ソーラーパネルのspiceモデルのパラメータをEXCELのソルバー機能を使い半自動で求めました。
GWソーラー製ソーラーパネルGW-E100のspiceモデルを電流-電圧特性(I-V特性)をもとにしています。
必要な知識は下記の通りです。
電子回路：LTspiceの基本操作、spiceの部品方程式(等価回路の知識)
統計：相関係数、決定係数
EXCEL：エクセル基本操作、EXCELソルバー
I-V特性 
P-V特性 
LTspiceの回路図とシミュレーション結果
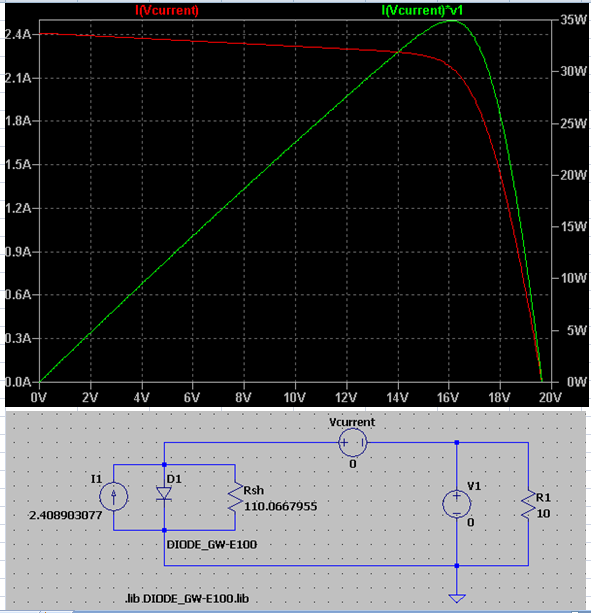
右：LTspiceのシミュレーション結果と等価回路図(パラメータ設定済み…Rs(後述)の抵抗なし)
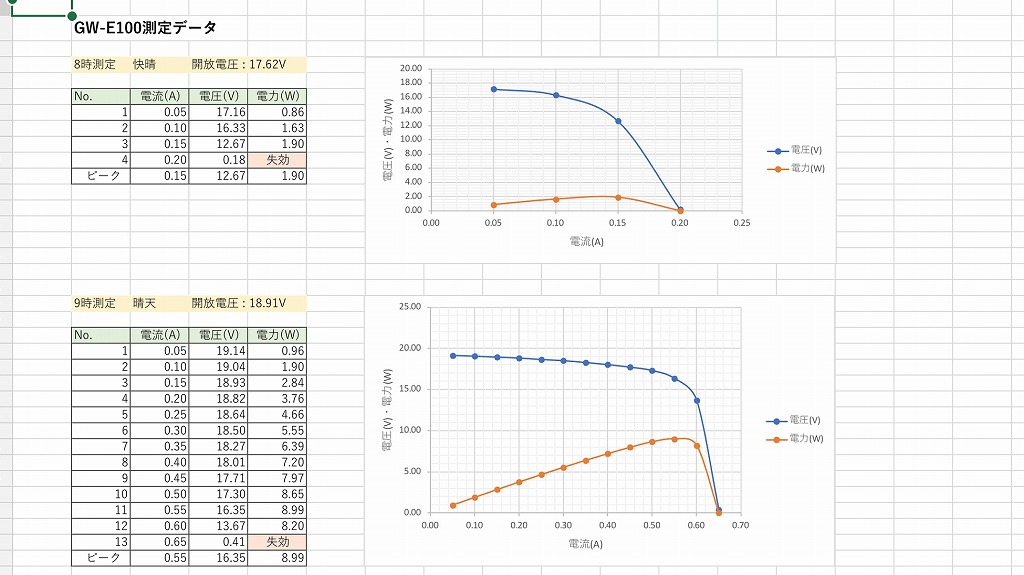
GW-E100の電流-電圧特性(I-V特性)・電力-電圧特性(P-V特性)のデーターシートは公開されていません。
そんな中、ありがたいことに、@EN_gelou様(Twitter)が計測頂いたデータを公開頂いています。
また、@EN_gelou様のご厚意によりデータの使用および公開許可を頂くことができました。
@EN_gelou様の元Twitterはこちらです。
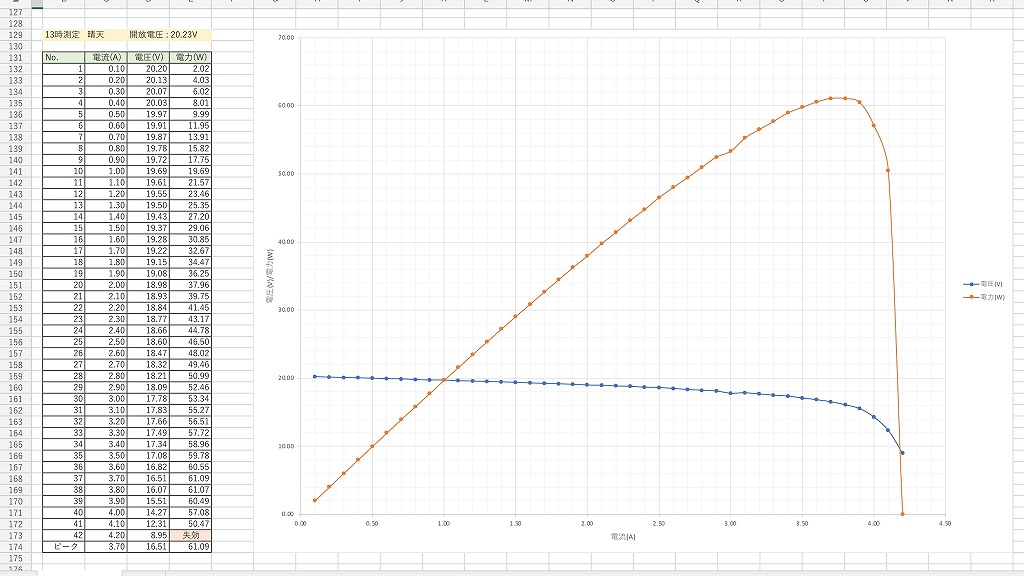
また、下記のデータも公開許可を頂きました。
データの諸元
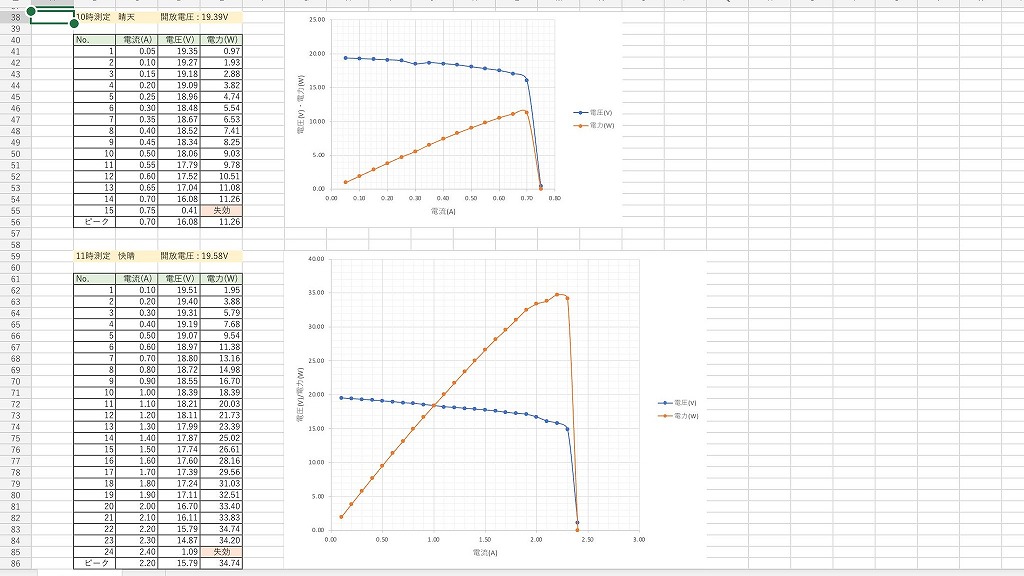
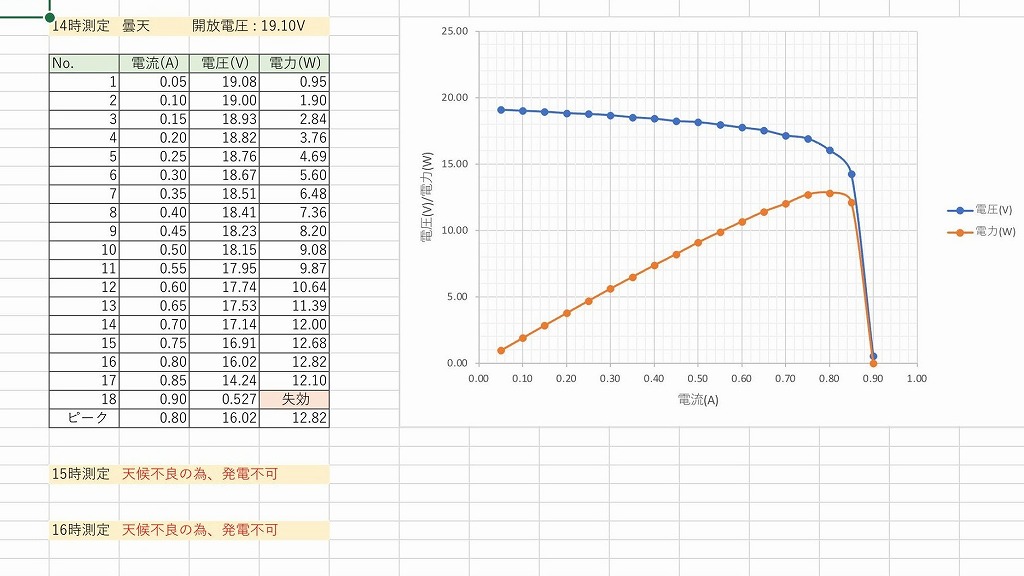
- データはAM11時のものを使用しています(画像の下側です)。
天候が快晴の状態でかつ、快晴時の出力の平均として解釈できそうなため(私の独断です)。 - 動作温度は27℃を想定しています。
パラメータ算出の簡便化のためです。
@EN_gelou様が測定頂いた時の気温は29℃でしたが、以下の2つの理由で29℃であることを無視しました。
・LTspiceのデフォルト温度が27℃としているため
・私がパラメータ決定のEXCELでダイオード・抵抗類に温度補正式をまだちゃんと加えていないため(今後もそこまでやるか不明です) - 太陽光の入射角度は65°を想定しています。
本来はソーラーパネルの特性でAM1.5(太陽角度θ＝41.8°)の入射角度が必要ですが、実測の測定条件として厳しいためです。
@EN_gelou様が画像を公開頂いた当日の週が8/10の週であったため、そのまま8/10の角度としました。
太陽の入射角度は音と色と数の散歩道様で確認しました。
参考書
LTspiceの部品モデルの自作は下記の参考書を参照しました。
参考書の内容はざっくりいうと下記の通りです。
- LTspiceの自作モデルの作り方
- それぞれの部品を把握するための最低限度の知識の説明
- 部品の等価回路の説明
- 部品の動作を再現するために調整するパラメータの説明
- パラメータ調整したspice部品をシミュレーションした結果と実部品のオシロスコープ画像の比較
参考書はspiceの部品モデルの自作をはじめたい！と言う方にはとても最適です。
理由はspiceモデルの自作について、たくさんの部品に対して統括的に説明した日本語の参考書はほとんど見当らないからです。
(トランジスタといった1点集中で説明している参考書はあります)
ただし、読んでみて問題点があると感じました。
次の章でお話しします。
参考書の問題点と対策
問題点は1点で、この本をもとに部品を作ろうとするともの凄い時間がかかることです。
手作業が前提になってしまうのです。
じゃあなぜ手作業前提かというと、一番かなめとなるspiceパラメータの決定を別ソフトPspiceのパラメータ抽出ツールPspice Model Editorに任せてしまっているからです。
また、Pspiceは無償版がありますが、無償版のPspice Model Editorで再現できるパラメータはダイオードしかありません。
幸いにも今回のようなソーラーパネルGW-E100のspiceモデルはダイオードが等価回路としてあるため、無償版を使えばパラメータの抽出は可能です。
しかし、今後いろいろな部品を再現したい場合、有償版のPspiceを入手する必要がありますが、いかんせん価格は高額で個人では手が出せません。
上記の対策として、パラメータ決定にEXCELのソルバ―で解決させることを試みました。
そのためには部品による波形の挙動がspiceでどのように再現されているか、原理原則を把握する必要がありました。
つまり、対象となる部品はどのようなspiceでどのような回路構成をもち、どういった理屈(例えば数式)を使っているのか、ということになります。
結局、エンジニアはものづくり・IT関わらず全て基本に通ずる、ということになります。
余談ですが、逆の発想からみれば、お金をかければ基本を身に着ける時間をとばすことができる、ということになりますね。
仕事の場合は時間の制約もでてきますので、時間をかけて基本をみにつけるか、原理原則はよくわからないが道具として使えれば良いか、case-by-caseになっていきます。
パラメータ決定の手順
今回のソーラーパネルGW-E100のパラメータは以下の手順で決定します。
- モデルの対象となる部品の原理原則を理解する(今回はソーラーパネルGW-E100が対象)
・基本動作
・LTspiceでシミュレーションするための等価回路と特性式を把握する
・等価回路の素子の特性式を把握する - LTspiceのパラメータがどこに対応しているか把握する
- EXCELソルバーでLTspiceのパラメータを動かし、ソーラーパネルの実測データの波形に近づけさせる
- ライブラリファイルの作成
- うまくいくまで③と④を繰り返す
- 実際にLTspiceでシミュレーションして実測した測定結果と確認
上記の手順は部品がソーラーパネルに限ったことではないと考えます。
それでは順番に見てきます。
①モデルの対象となる部品の原理原則を理解する
基本動作の把握(現象の把握)
まず、LTspiceモデルを作成するためにソーラーパネルの電気的特性を理解する必要があります。
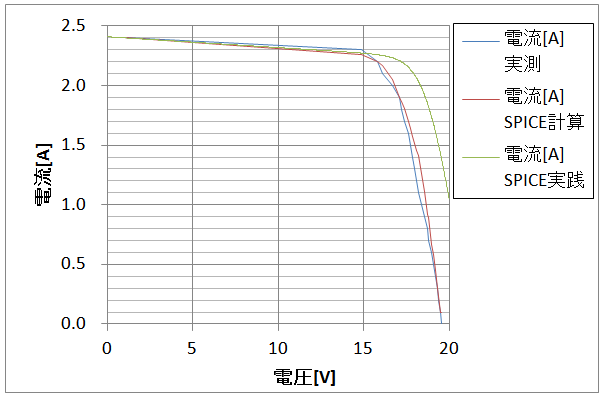
ソーラーパネルの場合、電流－電圧特性(I－V特性)になります。
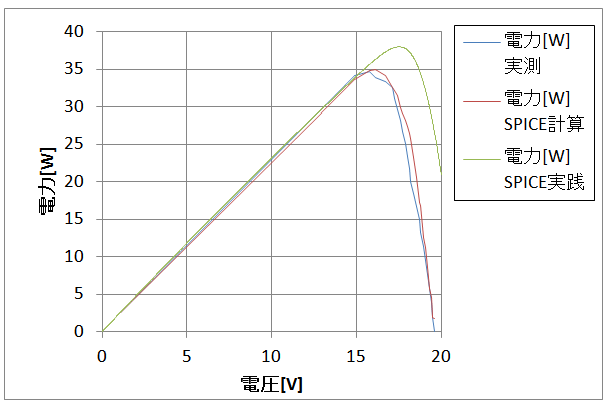
もうひとつ、電力－電圧特性(P-V特性)がありますが、シミュレーションのパラメータを求める場合はどちらもいっていることは同じになります。
(電力－電圧特性の場合、P=IVで電流Iを間接的に求めます)
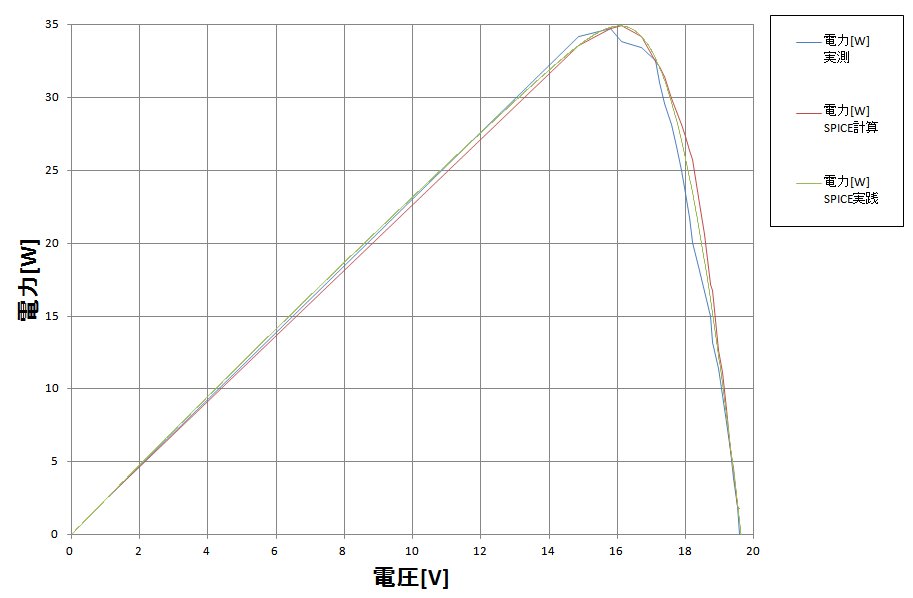
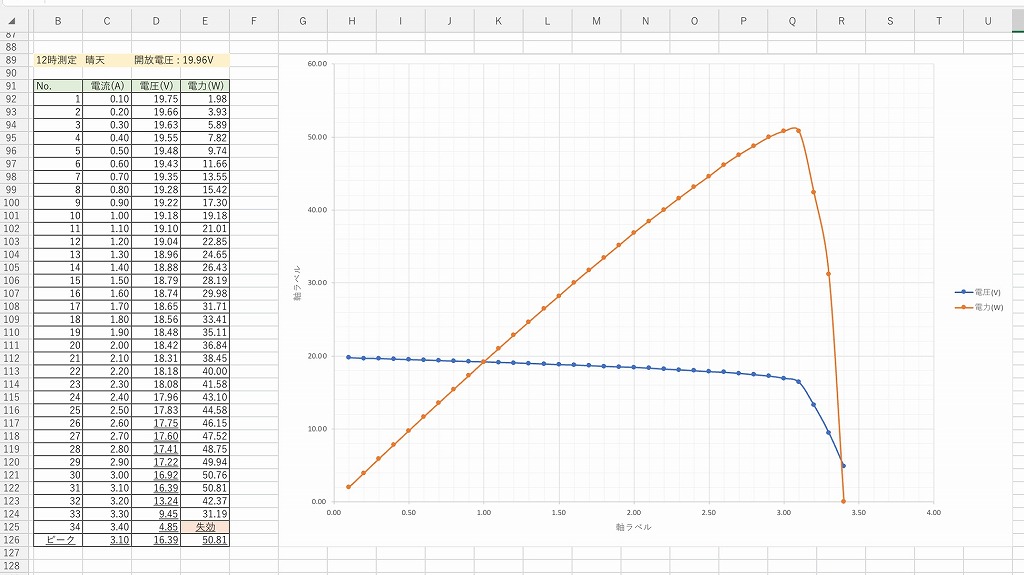
電流－電圧特性(I－V特性)と電力－電圧特性(P-V特性)を再掲します。
基本動作(現象)は参考書だけでなく、ネットにも基本動作の説明はたくさんあります。
マルツ パーツ様のHPに豆知識のレベルを超えてる内容でソーラーパネルの基本がまとめてあります。
LTspiceでシミュレーションするための等価回路と特性式を把握する
パラメータの説明は下記の通りです。
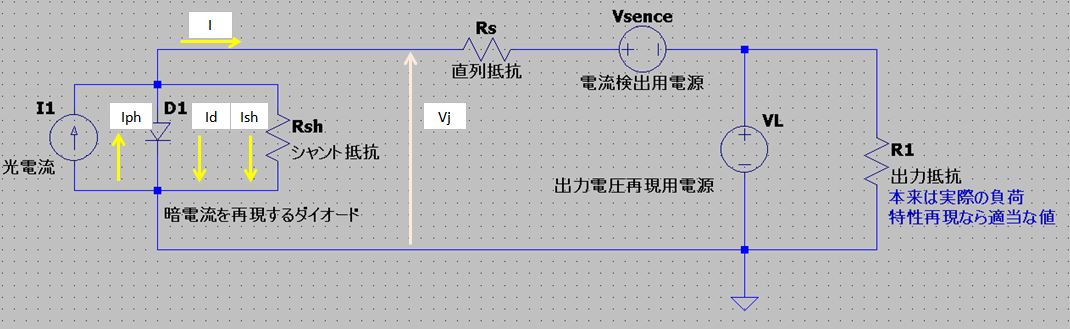
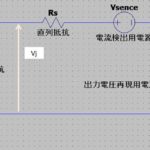
冒頭で示した等価回路の正式版はこちらです。
ソーラーパネルの等価回路図(全体) 
ダイオード等価回路(ソーラーパネルVer)
Iph：光電流
D：暗電流を再現するダイオード
Rsh：シャント抵抗
Rs：直列抵抗
等価回路の特性式(電流のつりあい)は下記の通りです。
この段階は参考書や検索エンジンで調べれば沢山でてきます。
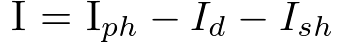
ソーラーパネルの電源は電流源(光電流)です、そのため電流からそれぞれのノードの電位を求めています。
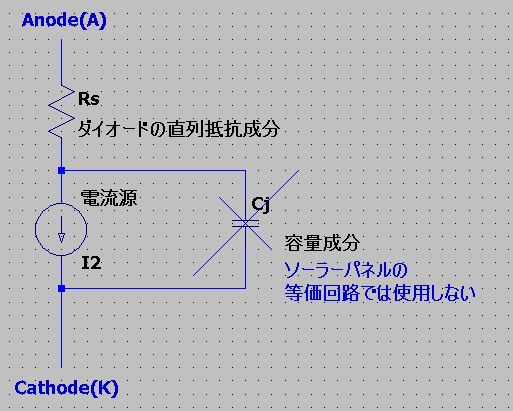
また、ダイオードはさらに等価回路があります。
次の節で説明します。
等価回路の素子の特性式を把握する
もし初めてこの等価回路を見た方なら、気になるところはダイオードではないでしょうか。
半導体に関わっているいるかた以外は目に入らない式なんじゃないかと思います。
ソーラーパネルのダイオード成分は暗電流(コトバンク様のHPに飛びます)を表す式となります。
ダイオードの等価回路でいえば、抵抗Rsと電流源の部分になります。
リカバリ電圧(逆回復特性)の現象を再現するコンデンサ成分Cjは、ソーラーパネルでは考えないため無視します。
上記の条件をふまえた式が物性式の第2項となります。
ソーラーパネルの特性式(物性－ダイオード成分は第2項) ダイオード等価回路(ソーラーパネルVer) ソーラーパネルの等価回路図(全体)
Is：飽和電流[A]
q ：電子の電荷…1.60218E-19[C] 【一定】
k： Boltzmann 定数…1.38065E-23[J/K] 【一定】
n ：ダイオード因子[単位なし]
T：測定温度(絶対温度)[K] 【0℃＝273K】
Vj＝(VL-Rs*I)：ダイオードにかかる電圧[V] 【ソーラーパネルの等価回路を参照】
※VjのRsとソーラーパネルの等価回路にあるRsを混合しないようにしてください。
※q, kは正確な値ではありません。
今回のパラメータ決定に問題がないであろう小数点の桁数を独断で決めました。
こちらもネットで検索すると正しい値がみつかります。
より細かい内容を知りたい場合、私が前職ではよく重宝させて頂きましたJEEA様のHPを紹介します。
基本式から太陽光システムの概要まで説明頂いています。
要点を短く述べています。
電子回路のシミュレーションにおいて一番の壁は、半導体部品の再現となります。
今回のソーラーパネルは半導体部品の再現の壁に対するトレーニングとしても最適だと思います。
半導体の動作特性の再現において、もっとも基本となる式と考えているからです。
②LTspiceのパラメータがどこに対応しているか把握する
等価回路と特性式を把握したら、次は特性式でどこの係数がLTspiceのパラメータと対応しているかを把握します。
下記に対応を示します。
特性式(物性)_電流 
対応式 
ソーラーパネルの等価回路図(全体)
それぞれの対応式の各項に対するパラメータは下記の通りです。
光電流Iphが電流源の値となります。
VL＝0の時の電流(短絡電流の時)に相当します。
(ソーラーパネルの物性式から分かる通り、厳密には違います)
ダイオードに関する部分はLTspiceに関係するパラメータを赤色で明記しています。
Is：(逆)飽和電流[saturation current]
N：ダイオード指数[Emission coefficient]
※実際の素子と理想的なPN結合の差異を修正するために使用する係数。
Ideality Factorとも呼ばれる。
※通常1~2の間をとるが、ソーラーパネルではこの限りではない模様。
参考書も形式HEM125PAのNを1.1374kとしている。
Rs：半導体バルク、オーミックコンタクトの接触抵抗などを含めた直列抵抗[Ohmic resistance]
IKF=0：高注入 knee 電流 [High-injection knee current]
※ダイオードのI-V特性(正式には順方向特性といいます)の傾きを調整するときに使用する。
参考書より今回はIKFが不使用のため、IKF=0。
上記、角カッコ”[ ]”はLTspiceのヘルプにある名称です。
正直それだけでは情報が足らなさすぎるので、金沢大学教授 北川章夫様のHPの内容を参照させて頂きました。
LTspiceのヘルプよりも非常に詳しく説明頂いています。
関係するパラメータはRsとRshになります。
Rsは電圧Vjに含まれています。
細かく言うと下記になります。
Rshには電圧Vjがかかっています。
電流値IshはVj / Rshとなります。
Vjは等価回路図の電流から電位差を求めると、VL-Rs*Iとなります。
そのためVj / Rsh＝(VL-Rs*I)/Rshとなります。
あとはパラメータ調整をしていきます。
③EXCELソルバーでLTspiceのパラメータを動かし実測と波形を一致させる
今回のハイライトです。
色々と工夫をしました。
EXCELソルバーで行うのは最小二乗法によるカーブフィッティングになります。
最小二乗法はもとデータの波形をそのまま合わせこむようなことはしないため、誤差を含むデータの近似方法に適しています。
カーブフィッティングについては露本伊佐男様のブログが分かりやすかったため、参考にさせて頂きました。
もちろんこちらもネットで検索すればたくさん内容がでてきます。
(大学のページが本質をついているためGoodです)
電流-電圧特性の実測プロットをまとめ、LTspiceのパラメータを対応させた式を、項ごとに作成していきます。
カーブフィッティングに相関係数、決定係数を利用する
今回は実測値をもとに特性式のカーブフィッティングを行います。
実測データに対しそのままEXCELソルバーをかけると、再現されるのは実測値の波形になってしまいます。
実測データは色々な誤差要因(計測器の誤差などモロモロ) を含んだ結果であるため、そのままシミュレーション用に使用するのは勇気がいります。
今回は「実測値から本来の特性式へあわせこむ」という方法をとりました。
そこで、相関係数・決定係数は統計の考え方を使いました。
以下、2つの用語の説明です。Wikipediaから引用しました。
相関係数（そうかんけいすう、英: correlation coefficient）とは、2 つの確率変数の間の相関（類似性の度合い）を示す統計学的指標である。
Wikipedia「相関係数」
原則、単位は無く、-1 から 1 の間の実数値をとり、1 に近いときは2 つの確率変数には正の相関があるといい、-1 に近ければ負の相関があるという。
決定係数（けっていけいすう、（英: coefficient of determination、R2）は、統計学において、独立変数（説明変数）が従属変数（目的変数）のどれくらいを説明できるかを表す値である。寄与率と呼ばれることもある。
Wikipedia「決定係数」
標本値から求めた回帰方程式（モデル）のあてはまりの良さの尺度として利用される。
spiceで使用する場合、次のようになります。
○相関係数
実測値とEXCELソルバーがだす計算の電流値の相関係数に着目している。
値が大きいほど、実測の電流値と等価回路の電流値が一致していることを示す。
この段階ではまだ等価回路の式が実測と一致していることを示していない。
○決定係数
値が大きいほど、実測の値から等価回路の特性式が一致していることを示す。
また、今回は決定係数＝相関係数^2の関係を使用した。
決定係数は複数の定義があります。
そのため必ず決定係数＝相関係数^2という関係ではありません。
今回は相関係数^2の定義がパラメータ決定におあつらえ向きだ、というだ考えで使いました。
こちらもネットで検索すれば大学の研究室の教授が解説頂いています。
(統計関係だと不確かさの影響がモロでる心理・経済・生物あたりでしょうか、勘ですが！)
今回の動画ではさらに決定係数^2しているセルがありますが、数値的な意味はありません。
私が勝手に、さらに精度よくパラメータの決定ができるのでは、と解釈して作った式です。
動画のEXCELソルバーでも、相関係数^2の方を使用しています。
話がそれますが…。
機械学習の分野でも決定係数を使う場合があります。
決定係数が大きすぎる(0.8より大)と「過学習」という状態になり、あるパターンの認識には強くなりますが、それ以外のパターンの認識は弱くなったりします。
決定係数はいつでも大きければ大きいほどよい、と言うわけではありません。
spiceパラメータ決定においては、特性式に限り限りなく近づけることが目的だから、大きければ大きいほど良い、という解釈になります。
手法を使うときは、必ず、できるだけでいいので根拠を明確に。
言葉ひとつ、係数一つで表される事象が大きく変わります。
それが物性式の難しさであり、おもしろさでもあります。
ながくなりましたが、使用する手法は使用する場面に応じ、最も適しているであろう解釈を選定し、使用しましょう、という事が言いたかったです。
と偉そうなことをいいましたが、わたしも現実では仕事に追われており薄い根拠をエイヤで出している身でもあります。
そのため自戒の意味を込めています。
EXCELソルバーの条件式
現実にありえない値を出さないために、以下の条件をつけています。
実測値と合わせこむ時はほとんどの場合で終息せずに計算がとまりますが、EXCELソルバーを限界まで追い込むためにやっているためです。
あまりに追い込み過ぎると機嫌を損ねて指定した条件をはずして勝手に適当な値を入れ始めますのでご注意ください！
飽和電流IsでEXCELソルバーの変化させる値を係数とべき乗数に分ける
飽和電流Is＝○*10^(-△)の式でEXCELソルバーが変化させる値を○と△でわけました。
Isは非常に小さい小数点の値(1*10^(-10)オーダー)になるためです。
実際に直接Isを操作しようとすると、EXCELソルバーがうまく数値を変化させることができませんでした。
(Is=0になってしまうことがしょっちゅうでした)
また、△の部分もEXCELソルバーをかけると小数点の値となり、人間から見ると違和感アリアリですが、Is自体は非常によい数値を出してくれるようになります。
調整するパラメータは実際に存在しうる範囲に条件付けする
抵抗Rs,Rs≧0といった具合です。
EXCELソルバーのオプション設定
次の画像の通りです。
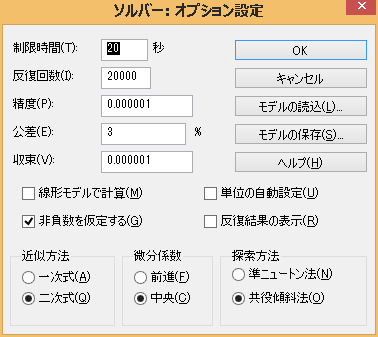
ぶっちゃけていえば、ほとんどが勘です。
パラメータを設定するときに相当復習をしたのですが、感覚で何となくわかっているだけで、まだ言語化できていません。
EXCELソルバーをこれでもかと追い込むねらいで、出力結果が終息しないほど厳しい値で設定しています。
制限時間：適当。この時間があれば十分でしょう、という勘です。
反復回数：適当。この回数があれば十分でしょう、という勘です。
精度：調整したらこの値が大体OKでした。つまり結果論、勘です。
公差：デフォルトの5%じゃゆるいかなぁ？という気持ちです。つまり勘です。
収束：キッツンキッツンに追い込んでやろう、という気持ちです。つまり勘です。
非負数を仮定するにチェック：セルの値の条件で≧0の値の設定漏れがあった場合の対策です。
近似方法：対象となるカーブは非線形のため「二次式」にしています。
微分係数：制約条件の値が比較的ゆるやかに変化しないものと考えて「中央」にしています。
探索方法：私のPCがショボいため、メモリのやさしさを優先したく「共役傾斜法」にしました(石橋を叩きまくっています。本来なら収束性がよい準ニュートン法が良いです)。
※「線形モデルで計算」はチェックをしないようにしましょう。
今回の式は線形ではありません。エラーになります。
各項目の説明は内容が長くなってしまうため割愛します(参考書1冊分らくにいきます…！)。
細かい内容はネットで検索して調べてみてください。
はじめにある程度、手作業でパラメータを変更して波形を実測にある程度合わせる
今回私はEXCELソルバーで共役傾斜法を設定したためです。
共役傾斜法の特性上、事前に手作業である程度波形を合わせてあげる必要があります。
また、最小二乗法はソルバー動作中は極値を探すだけです。
あまりに適当な初期値でソルバーを走らせるとデタラメな結果で収束しますので注意です。
次の動画に例を示します。
EXCELを作成している途中のものです。
この時のEXCELで飽和電流Isは係数とべき乗数にわけていませんが、値は決定してくれました。
それでも、相関係数が負の相関となっており、そこで収束してしまっています。
(このあと、EXCELソルバーの条件に相関係数R≧0も追加しています)
準ニュートン法の場合はまだ試してませんので、機会があれば追記する予定です。
(設定変えてやるだけやろ！というツッコミがくるだろうか…！？)
④ライブラリファイルを作成
他の型番のソーラーパネルで今回の等価回路を使いまわしやすくするため、ダイオードのパラメータは以下のフォルダにライブラリで登録します。
ライブラリファイルの作成方法はMONOist様のHPに記載があります。
ライブラリファイルが完成したら、フォルダC:\Users\「ユーザ名」\Documents\LTspiceXVII\lib\subにlibファイルを保存します。
※「ユーザ名」は自分のPCにログインしたユーザー名のことです。
※デフォルトではCドライブのProgramFilesのフォルダにあるライブラリファイルは読み込み専用で保護されているため、個別ユーザのLTspiceフォルダで登録します。
拡張子は.libです。
デバイス名は人間側がみて分かりやすくするため、自作した等価回路のダイオード名に統一します。
本来、たしか、どこか1か所だけ名称を合わせる必要なしだったはずですが…。
ややこしくなるため、あわせました。
⑤うまくいくまで③と④を繰り返す
EXCELソルバ―は共役傾斜法で設定しているため、一回では上手くいくことはまれです。
実測の波形に終息しなければ、再度一部のパラメータを手作業でいじってソルバーを回していきます。
どのパラメータをいじれば、どこの波形が動きやすくなるか、ひとつずついじってみて確認してみてください。
参考書に各パラメータの変更に対して波形がどのように変化するかが書いてありますが、実際に手を動かした方がより感覚をつかめますし、確実です。
⑥実際にLTspiceでシミュレーションして実測した測定結果と確認(注意点も)
LTspiceでシミュレーションを行います。
ここで一つ注意点があります。
今回のパラメータ設定条件で、飽和電流Isのパラメータは×10倍した値を入れましょう。
(他のソーラーパネルでも当てはまるかは確認要です)
EXCELソルバーで求めた波形とLTspiceの波形を比較したら、見た目は相似の波形になっていたため、色々パラメータをいじった結果、Isを×10倍して一致した、という結果論です。
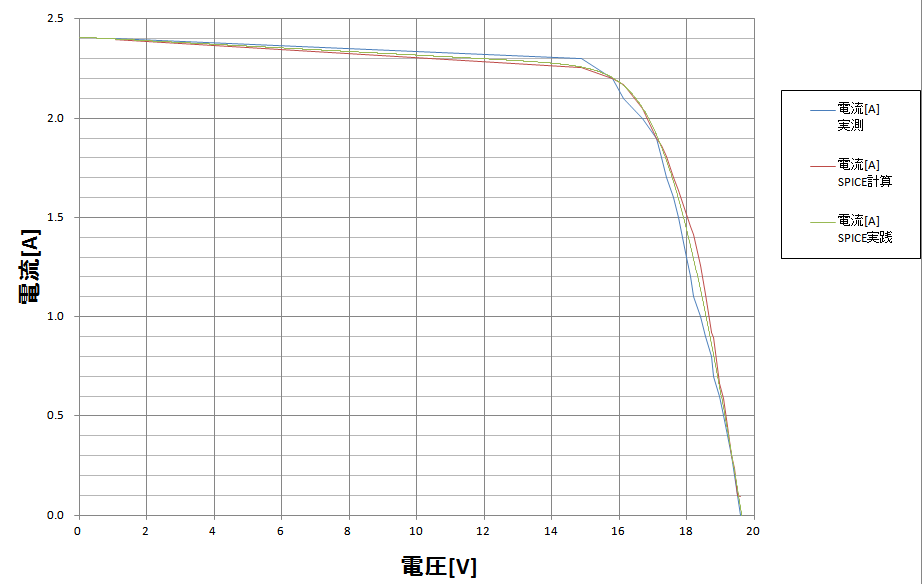
出てきたシミュレーション結果をテキストに落とし、ソルバーのEXCELで作成したグラフに入れ込んでみて気づきました。
グラフは次の通りです。
I-V特性_比較_計算結果そのまま代入 
P-V特性_比較_計算結果そのまま代入
カーブが折れまがるタイミングが違うだけで、途中は一緒です。
こういう時は非常に違和感しかありませんし、あと一歩という根拠のない直感がでてきます(外れていることも多いですが！)。
原因はLTspiceの内部計算式の影響では、と考えています。
また、設定していないパラメータの影響もあるのでは、とも考えています。
何にせよ、もっと詳細のモデル式の調査が必要と考えてもいます(いつやるか…)。
以上の点を気をつけると、冒頭で示したようにソーラーパネルGW-E100のI-V特性(P-V特性)が再現できます。
下記に飽和電流Isのパラメータを×10倍してシミュレーションした結果を再掲します。
LTspiceの回路図とシミュレーション結果 i-V特性 P-V特性
今後の方針
- 他のソーラーパネルも今回の方法で再現可能か確認
【2021/1/18】
測定したデータがあれば、パラメータの初期値を何回か調整でできる。 - 実際に方程式を解いてパラメータが再現可能か確認
私の持論ですが、ものづくりエンジニアは数式を扱えてエンジニアです。
今回はEXCELソルバーでパラメータを求めましたが、I-V特性の波形にあうパラメータなら何でもよいことになり(パラメータは複数パターンが許されるため)、乱暴です。
本来はソーラーパネルの製品の固有値(パラメータ)は1つのはずです。パラメータは一義にきまるべきです。
【2021/1/18】
色々な文献がありました。
どれも一筋縄ではいかない印象。
海外の論文が有力情報に行けると思いました。
【2021/5/20】
こちらの文献がシンプルかつプログラムが公開されていましたので採用しました。
メーカが公開しているソーラーパネルのデータシートから再現する方法です。
私がGumroadで販売しているモデルもこの内容を採用しています。
モデルが製作できる方は私のモデル購入のために余計なお金を払う必要はないと考えています。
是非実施してみてください。
A New Simplified Five-Parameter Estimation Method for Single-Diode Model of Photovoltaic Panels, November 2019 Energies 12(22):4271
まとめ
LTspiceでソーラーパネルGW-E100を例にして、実測したデータ(I-V特性)からspiceパラメータを求めることができました。
パラメータを決定するための手順は他の部品でも使えると思います。
工夫した部分はEXCELソルバーです。
最も工夫した個所は、誤差をふくんだ実測データから等価回路の特性式に当てはまり具合を相関係数・決定係数を用いて数値化したことです。
実際にやってみると等価回路はまだ良いのですが、半導体関係の特性式を探すことが難しいと感じると思います。
理由はspiceのルーツはアメリカだからです。
つまり、spiceの関連文書を探す場合は英語で検索することが前提と考えることをおすすめします。
英語が読めなくても大丈夫です。私もTOEIC280点です。
翻訳ツールなど利用して地道に理解しましょう。
なにより、私達ものづくりエンジニアの共通言語は英語ではありません。
現象を表す数式が本来の共通言語です。
さいごに、今回の内容がspiceシミュレーションに関わる皆さまの参考になったら幸いです。
ありがとうございました。
【2021/5/20】ソーラーパネルの温度特性を再現できました。
この記事では実測ベースのパラメータの算出方法ですが、次の記事はメーカのデータシートの値をもとに算出しています。
お試し版のライブラリファイル・シンボルファイルとモデルの性能レポートを置いています。
是非目を通して実際にシミュレーションしてみてください。
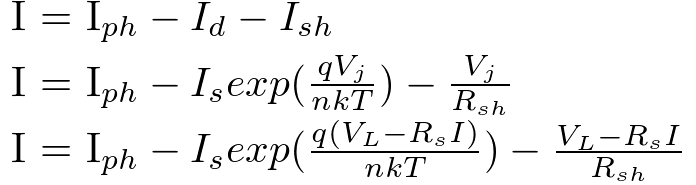
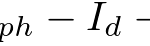
コメント スパム対応をしたつもり、コメントは残す方向で頑張ってます