ダイオードの逆回復特性をLTspiceで再現しました。順方向・逆方向のVf-If特性と容量特性(C-V特性)は維持しています。
再現対象は東芝製ダイオード1SS387(参考文献1)です。
25℃の常温の前提はありますが、今回の記事でダイオードの基本特性を一通り再現できたと思います。
↓Vf-If特性・容量特性の記事↓
まとめ
各特性の結果です。
クリックで拡大できます。
順方向・逆方向のVf-If特性と容量特性(C-V特性)は維持しつつ、逆回復特性の再現を確認しました。
【逆回復特性】
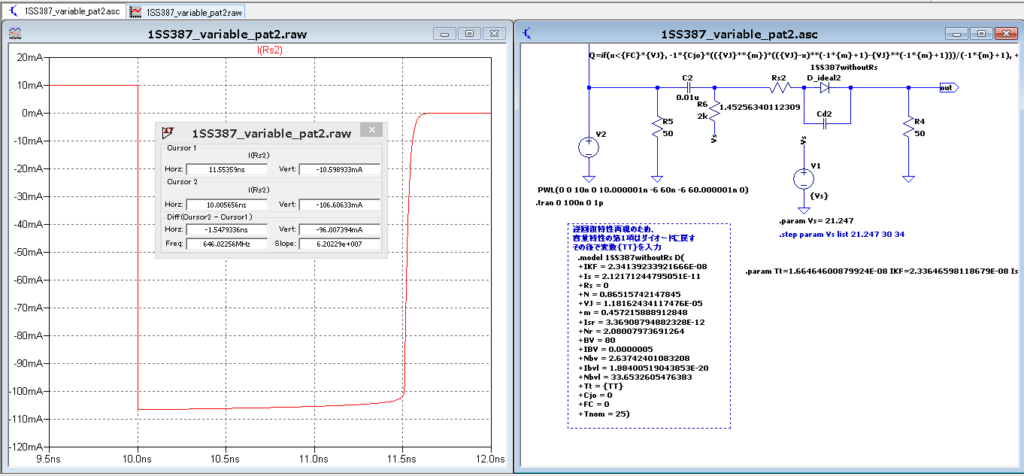
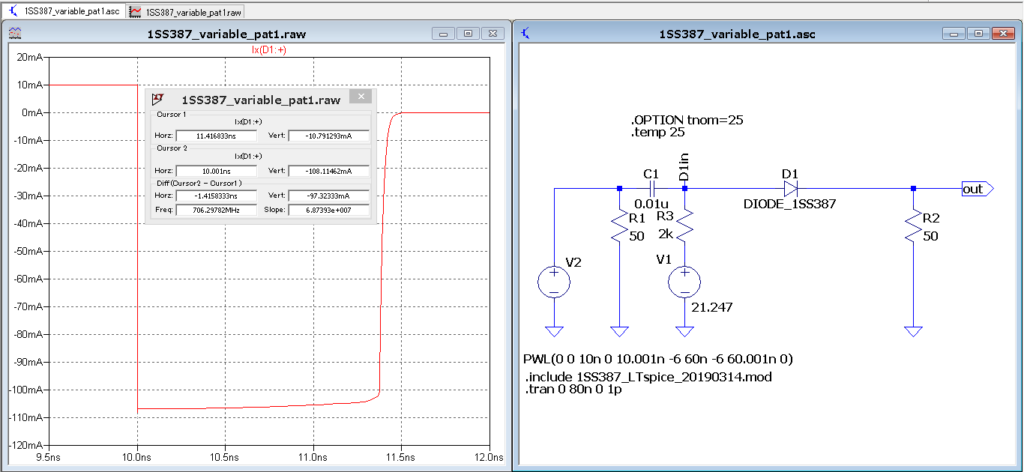
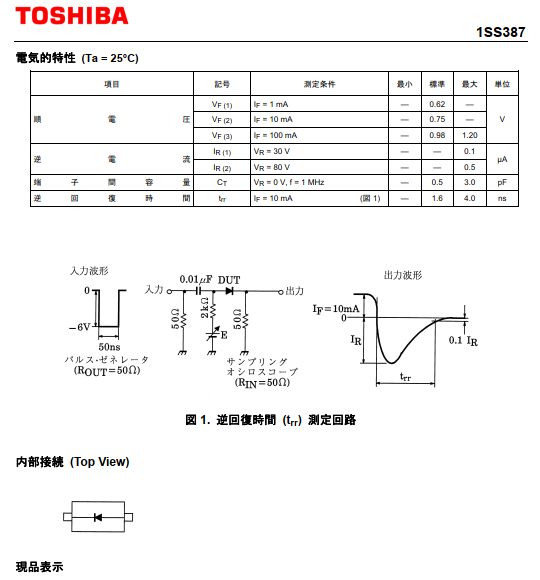
・前提:If...データシート10mA シミュレーション...10.001172mA
机上計算した\(\displaystyle {\color{red}{\tau_T}} \)(後述)を使用
・結果
データシート:1.600nsec ...データシートtyp値
結果:1.548nsec 逆回復時の電流Max値IrとIr/10になるまでの時間
本家:1.416nsec 同上
【順方向・逆方向のVf-If特性】
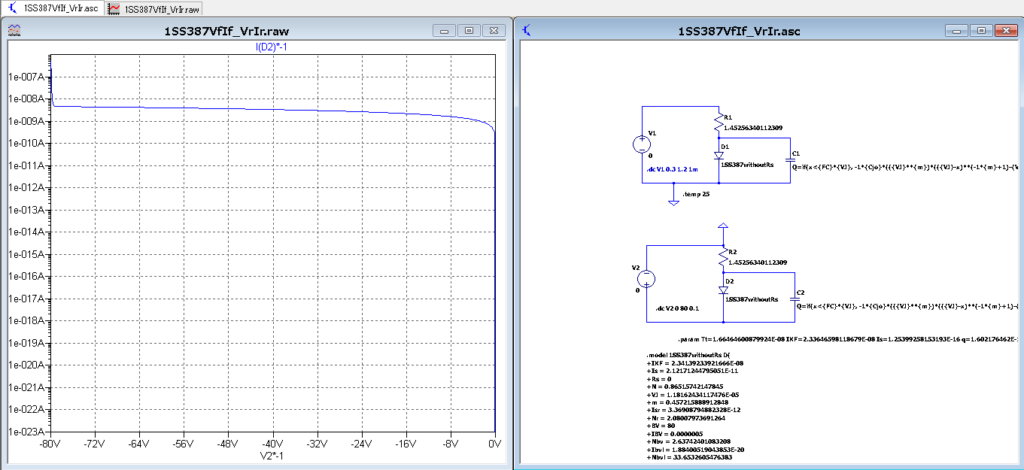
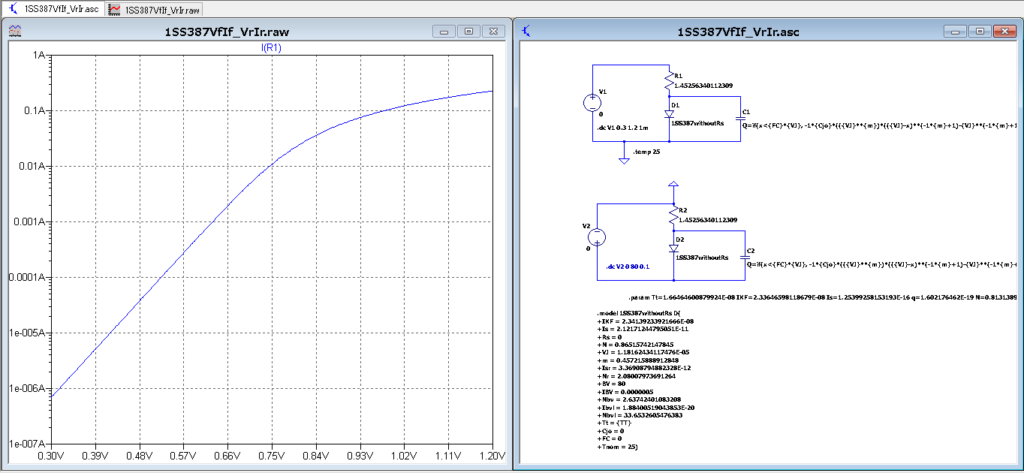
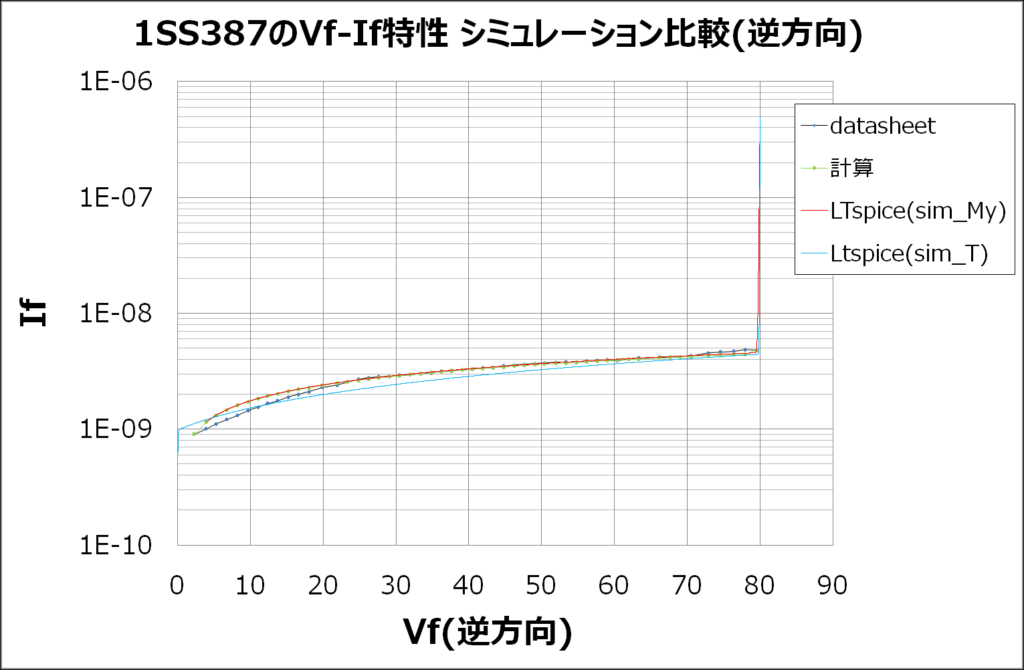
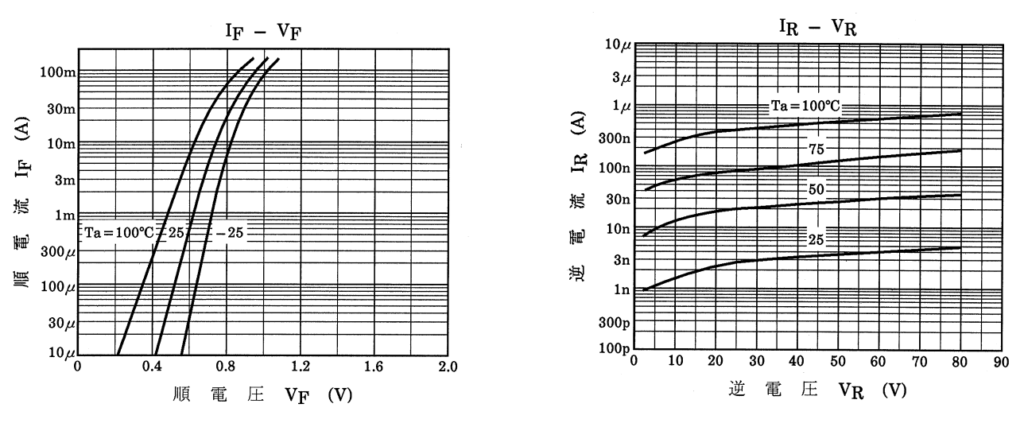
補足として、グラフの比較はSim_MYが自作モデル、Sim_Tが本家モデル(東芝製)となります。
【容量特性(C-V特性)】
●順方向特性
前回の記事で再現したC-V特性は上の凸がなかったのですが、パラメータ\(\displaystyle {\color{red}{FC}}\)を設定したことで本家モデルの動作にあわせるようにしています
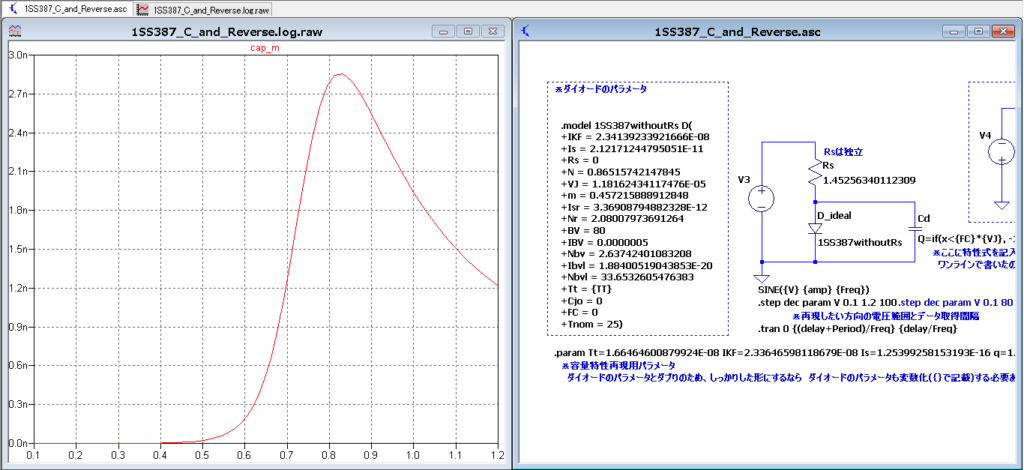
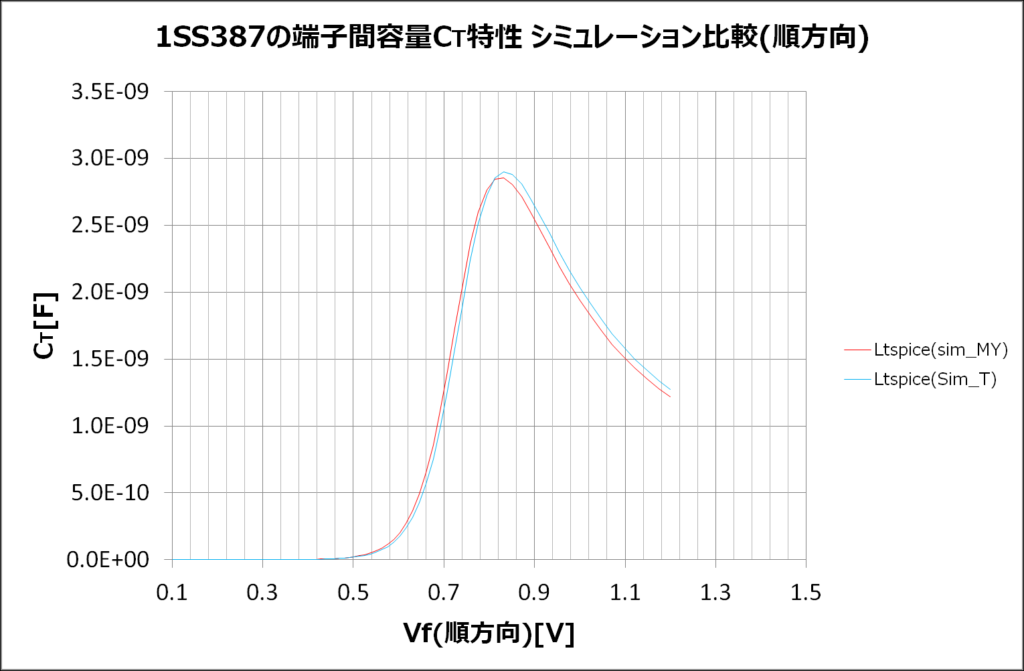
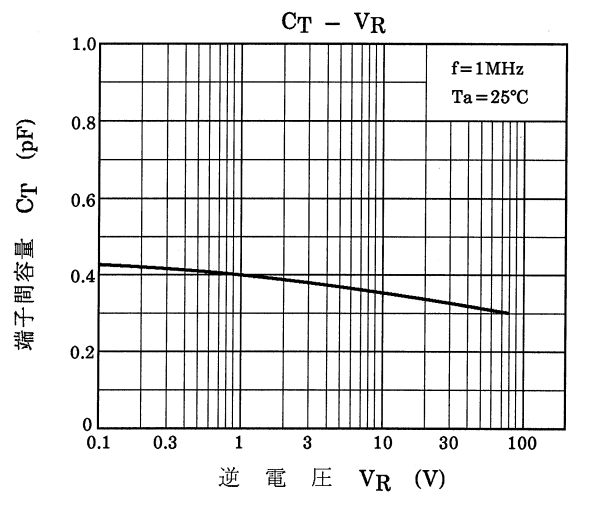
●逆方向特性
ダイオードにパラメータ\(\displaystyle {\color{red}{\tau_T}} \)をもどすことで、ブレークダウン電圧あたりの電流の急増による容量急増も確認できた 本家モデルと大体同じ挙動になりました。
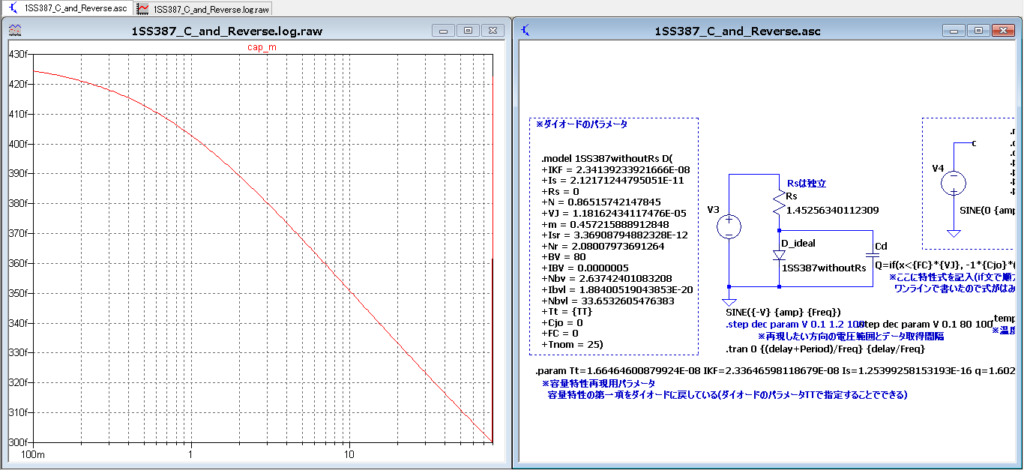
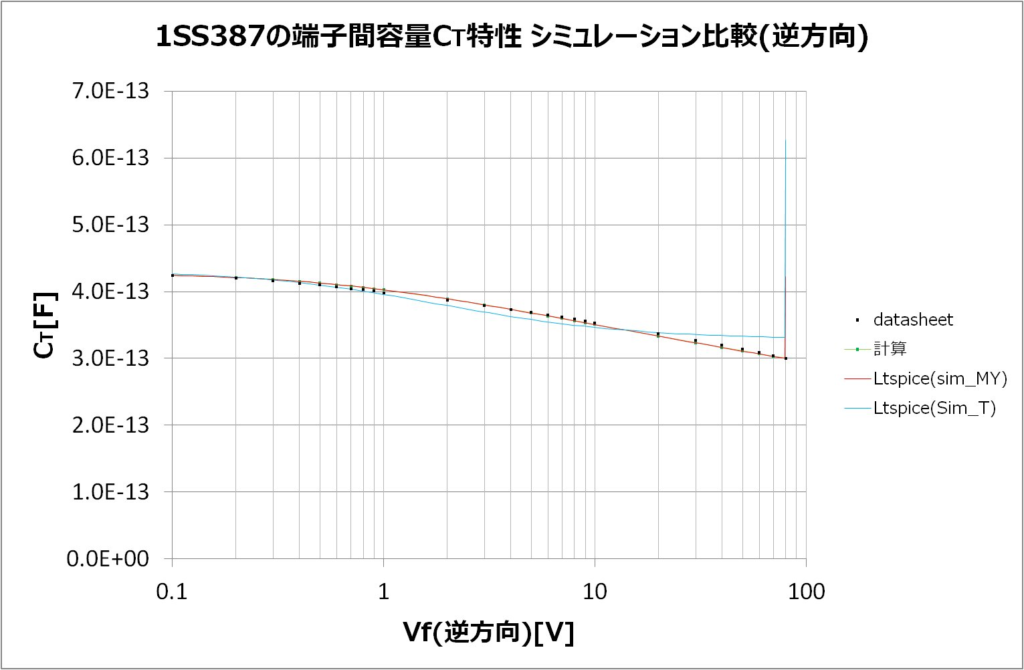
補足として、グラフの比較はSim_MYが自作モデル、Sim_Tが本家モデル(東芝製)となります。
理論(原理)
ダイオードの逆回復特性とは、と言った内容はググれば大量に情報が出てきますし、私がまとめるよりもはるかに分かりやすい説明になっていますので、基本的な内容は他のサイト様に委ねます。
ここでは、逆回復特性のパラメータに注目して述べていこうと思います。
逆回復時間のパラメータの関係式
LTspiceではダイオードの逆回復時間はパラメータ\(\displaystyle \tau_{off} \)(Transit Time)で設定します。
ただ、\(\displaystyle \tau_{off} \)の値がそのままデータシートの逆回復時間にはなりません。
\(\displaystyle \tau_{off} \)は逆回復特性の半分(波形立ち上がり前)までを再現します。
関係式は次の通りです。
\(\displaystyle \tau_{off}= {\color{red}{\tau_T}} * ln(1-\frac{I_F}{I_R}) \tag{1}\)
ただし、
\(\displaystyle \tau_{off} \):逆回復特性の逆回復時間[sec]
・求めたい時間...データシートに記載されている
\(\displaystyle {\color{red}{\tau_T}} \):Transit Time[sec]
・求めたいLTspiceパラメータ
・ダイオードn側の順方向電流におけるホール(正孔)の平均ライフタイム
\(\displaystyle I_F \):順方向電流[A]
\(\displaystyle I_R \):逆回復時に流れる電流値(ピーク)[A]
今回の東芝製ダイオード1SS387(参考文献1)の場合、私は次の通りに求めました。
\(\displaystyle \tau_{off} \):1.6nsec
\(\displaystyle I_F \):10mA
\(\displaystyle I_R \):約-99.120mA(※シミュレーション-106.6111mAと差異アリ)
ここで、\(\displaystyle I_R \)について詳細を下記に示します。
\(\displaystyle I_R \)は\(\displaystyle \frac{(-6+0.9)[V]}{(1.4525455497596+50)[Ω]} \)としています。
今回の回路であれば、\(\displaystyle I_R \)は逆電圧・理想ダイオードの電位差と抵抗値があればもとまりますので、とりあえずシミュレーションで逆回復特性を発生させ、プロット値(上記-106.6111mA)で読み取る方が正確だと思います。本来の正確なパラメータを求める意味でも、同様と考えます。
ただ、今回、私はこの方法はやらず、机上計算でざっくりアタリをつけるやり方としました。シミュレーションを走らせる前は自分が何を再現させたいか・回路上の電位の関係をダブルチェックの意味もかねて把握したかったからです。そのため、私が机上計算で求めた約-99.120mAはざっくりあたりを付けた値となります。
具体的には、上記逆方向電圧-6Vを印加した時のダイオード部とダイオードの寄生抵抗部をあわせた電位差を0.9Vとざっくり決めました。本来だったら電源が2つあるので重ね合わせの理から各部の電位差を地道にしっかりと求めるべきです。と、偉そうに言ってやりませんでしたが。
関係式に至るまでの詳細は次の通りです。
参考文献2より、順方向時に流れる電荷と逆回復時に流れる電荷のつり合いに着目します。
順方向電流量と時間の積(電荷量)、逆回復特性発生時の電流量(平均)と時間の積(電荷量)が等しくなることを考えます。
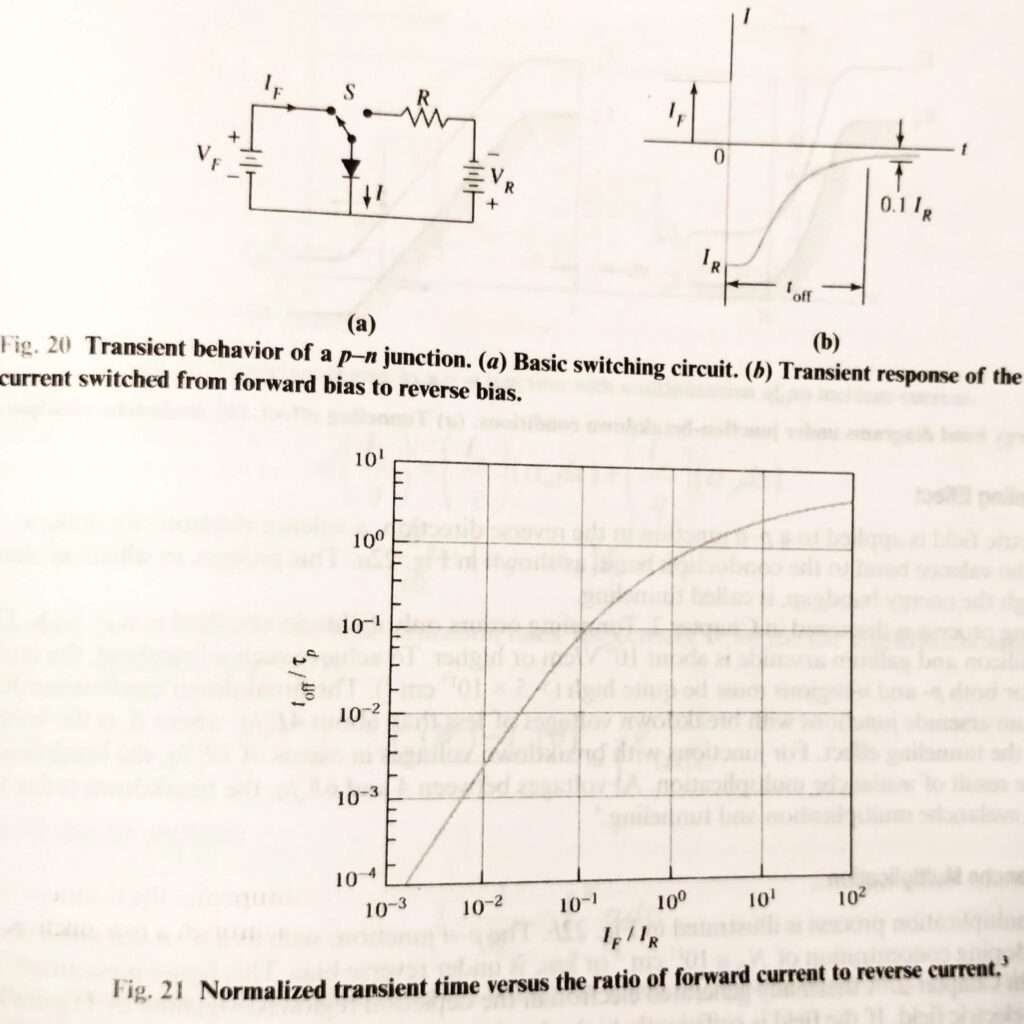
下図にダイオードの逆回復特性の基本回路図・特性図・電流比と逆回復時間の関係図を示します。
上記式(1)により、順方向電流が大きいほど逆回復時に相殺する電荷量がおおくなるため、順方向電流が大きいほど逆回復時間\(\displaystyle \tau_{off} \):\(\displaystyle I_{R}\)が発生してから10%となるまでの時間が長くなることが分かります。
Simon M. Sze(2012), Ming-Kwei Lee, Semiconductor Devices: Physics and Technology International Student Version Third Edition, WILEY, p111 ダイオードの逆回復特性_基本回路図・特性図・電流比と逆回復時間の関係図
図中の\(\displaystyle I_{R} \)はスイッチSが切り替わった後の抵抗Rに流れる逆方向の電流\(\displaystyle V_{R} / R\)です。
図では波形も電流の立ち下りがほぼ垂直落下→\(\displaystyle V_{R} / R\)となり、その後は”ほぼ”平坦を維持→ダイオードの内部RC成分による直列回路(と言ってしまいますが)による波形の立ち上がりとなります。
上記をふまえると、関係式は次のようになります。
\(\displaystyle {\color{red}{\tau_T}} * I_F = \tau_{off} * I_{R_{ave}} \tag{2}\)
パラメータの説明は次の通りです。冒頭の内容と重複しますが、ご容赦ください。
\(\displaystyle {\color{red}{\tau_T}} \):Transit Time[sec]
・求めたいLTspiceパラメータ
・ダイオードn側の順方向電流におけるホール(正孔)の平均ライフタイム
\(\displaystyle I_F \):順方向電流[A]
\(\displaystyle \tau_{off} \):逆回復特性の逆回復時間[sec]
・求めたい時間...データシートに記載されている
\(\displaystyle I_{R_{ave}} \):逆回復時に流れる電流値(平均)[A]
ここで注意することは、電流値\(\displaystyle I_{R_{ave}} \)が平均の電流値であることです。
そのため、実際の逆回復時の\(\displaystyle I_{R_{ave}} \)は次の2点の理由により簡単に求められません。
- ダイオードが短絡直後からしばらくの間の電流値はパッと見一定のように見えるが、そうではなく徐々に上がっているため(若干だが、誤差要因となる)
さきほど”ほぼ”と述べたのはこのため - RC成分があるため電流波形が非線形となるため(特にCの値は両端の印加電圧で常に可変となるため、紙の上でパッと計算できない)
そのため、参考文献3より\(\displaystyle I_{R_{ave}} \)を考えなくて良いように、ピーク電流値\(\displaystyle I_{R} \)をつかった次の式で近似しています。この章の冒頭で出した式です。
\(\displaystyle \tau_{off}= {\color{red}{\tau_T}} * ln(1-\frac{I_F}{I_R}) \tag{3}\)
今回は式(3)の式を使ってLTspiceのパラメータ\(\displaystyle {\color{red}{\tau_T}} \)を求めます。
シミュレーション結果は冒頭の章”まとめ”の通りです。
【補足】
今回のシミュレーションでインダクタは含めていません。
実際はSMD品であればパッケージの端子部であったり、リード配線が施されているタイプものは配線によるインダクタがあるため、電流の立ち下りは直角ではなくナナメの傾斜をもちます。
電流波形も逆回復時の立ち上がりでRLCにて共振するため、波形はオーバーシュートを含んだナミナミになります。
また、参考文献2の内容は電流の動作を示していますが、その時の電圧の挙動はありません。電圧を含めて確認したい方は参考文献4を参照してみてください。逆回復時のダイオード部の電位差は維持されているのが確認できます。
さらに、参考文献5では式(3)よりもさらに正確に\(\displaystyle {\color{red}{\tau_T}} \)を求めてる方法が記載されています(この文献は有料です)。本家である東芝製1SS387のモデルの特性と比較をしたかったため、やっていません。
容量特性の電荷式の分担(容量特性式の第一項をダイオードに戻す)
今回、逆回復特性を再現するにあたって、容量特性の式を変えています。
ダイオードのコンデンサ部の式"Q=〇〇〇〇・・・"の部分です。
具体的には、順方向・逆方向の共通部である特性式の第一項をダイオードに戻しています。
章「まとめ」の回路図にあるコンデンサ部の式"Q=〇〇〇〇・・・"を確認すると、下記式(4)(5)の第一項はなく、いきなり第二項からはじまっています。
第一項をダイオードに戻す戻し方は、次の通りです。
- \(\displaystyle \color{red}{\tau_T} \)はダイオードのパラメータとして入力
(ダイオードの特性式の第一項に相当) - 残りのパラメータはコンデンサの"Q=〇〇〇〇・・・"の方の式のパラメータの値として入力
順方向・逆方向の特性式を再掲します。式の最終部分のみです。
詳細は前回の記事で再現したC-V特性を参照してください。
ここで、\(\displaystyle \color{red}{\tau_T} \)は式中の\(\displaystyle \color{red}{\tau_{D}} \)に相当します。
【順方向特性】
\(\displaystyle Q_{D}=\color{red}{\tau_{D}}K_{hil}I_{D}+\color{red}{C_{j0}}F1+\frac{\color{red}{C_{j0}}}{F_{2}} \int_{\color{red}{FC}*\color{red}{VJ}}^{V_{diode}} \big(F_{3}+\frac{\color{red}{m}V}{\color{red}{VJ}}\big) dV \ \quad for \quad V_{diode} >= \color{red}{FC}*\color{red}{VJ} \tag{4}\)
ただし、\(\displaystyle \color{red}{\tau_T} \)は式中の\(\displaystyle \color{red}{\tau_{D}} \)に相当
この特性はデータシートに無い場合がほとんどと見受けられます。1SS387のデータシートにもありませんでした。その場合は参考程度の再現となります。
【逆方向特性】
\(\displaystyle Q_{D}=\color{red}{\tau_{D}}K_{hil}I_{D}-\color{red}{C_{j0}} \frac{\color{red}{VJ}^\color{red}{m}(\color{red}{VJ}-V_{diode})^{-\color{red}{m}+1}}{-\color{red}{m}+1} \quad for \quad V_{diode} < \color{red}{FC}*\color{red}{VJ} \tag{5}\)
ただし、\(\displaystyle \color{red}{\tau_T} \)は式中の\(\displaystyle \color{red}{\tau_{D}} \)に相当
手順
次の表の通りです。
順方向・逆方向のVf-If特性のパラメータは求まっている前提です。
| NO | 内容 | 補足 |
| 1 | 式(3)より \(\displaystyle \color{red}{\tau_T} \)を算出 | \(\displaystyle \tau_{off} \)・\(\displaystyle I_F \)・\(\displaystyle I_R \)(確認できれば)はデータシートを確認する |
| 2 | 求めた \(\displaystyle \color{red}{\tau_T} \)を用いて容量特性(C-V特性)のパラメータを計算 ダイオードの容量成分を分けてた"Q=〇〇〇〇・・・"の式のパラメータをだす | ・具体的な内容はこちらの過去記事(C-V特性再現)を参照 ・先に容量特性(C-V特性)を求めていたら再度計算する |
| 3 | それぞれNO1,2で求めたパラメータをLTspiceに描いた回路図のパラメータ欄に入力 前節”容量特性の電荷式の分担(容量特性式の第一項をダイオードに戻す)”を参照 | ・\(\displaystyle \color{red}{\tau_T} \)はダイオードのパラメータとして入力 (ダイオードの特性式の第一項に相当) ・残りのパラメータはコンデンサの"Q=〇〇〇〇・・・"の方の式のパラメータの値として入力 |
その他:パラメータVpについて
LTspiceのダイオードの逆回復時間は二つの時間のパラメータ\(\displaystyle {\color{red}{\tau_T}}\)と\(\displaystyle Vp\)をもっています。図1でいえば、\(\displaystyle {\color{red}{\tau_T}}\)は電流の立ち下り後から再び立ち上がるまでの時間パラメータで、\(\displaystyle Vp\)は電流波形が再び立ち上がった後の波形の形状パラメータです。
LTspiceには逆回復時の終盤で波形の立ち上がり形状をきめるパラメータ\(\displaystyle Vp\)があります。実際の波形のイメージは参考文献3の後半にあります。
実際に\(\displaystyle Vp\)を調整して電流波形が再び立ち上がった時の波形の形状を確認頂いた方がいます。大変参考になります。通常のリカバリーからソフトリカバリーまでパラメータの調整で行えるようになっていると見受けられます。
また、\(\displaystyle Vp\)のより詳しい内容は参考文献6(LTspice Help)にで引用されている文献”K.J. Teng and S. Pan in 'Modified charge-control equation for simulation of diode reverse recovery', Electronics Letters, 15th February 1996 Vol. 32 No. 4.”を参照してください(この文献も有料です)。
今回の特性再現では\(\displaystyle Vp\)は使用していません。時間\(\displaystyle {\color{red}{\tau_T}} \)のみを使用しています。
\(\displaystyle Vp\)は調整していません。本家である東芝製1SS387のモデルの特性と比較をしたかったためです。
機会があれば\(\displaystyle Vp\)の話は追加できたらなと思います。機会があれば。機会があれば。
参考文献
- 1SS387(2022), 東芝デバイス&ストレージ株式会社
https://toshiba.semicon-storage.com/jp/semiconductor/product/diodes/detail.1SS387.html - Simon M. Sze(2012), Ming-Kwei Lee, Semiconductor Devices: Physics and Technology International Student Version Third Edition, WILEY, p110(Eq80)
- How to model reverse recovery diode in LTSpice?, Electrical Engineering
https://electronics.stackexchange.com/questions/641280/how-to-model-reverse-recovery-diode-in-ltspice - Electronic Circuits - Diode as a Switch, Tutorials Point, India Private Limited
https://www.tutorialspoint.com/electronic_circuits/electronic_circuits_diode_as_switch.htm - Denys I. Zaikin(2015), Basic diode SPICE model extension and a software characterization tool for reverse recovery simulation, 2015 IEEE International Conference on Industrial Technology (ICIT), IEEE
https://dx.doi.org/10.1109/ICIT.2015.7125218 - D. Diode、LTspiceHelp, Analog Devices Inc, 1998-2022
変更履歴
記事UP
・サムネイルUP
・章「まとめ」:下記、参考文献1:データシート参照の内容を追加
逆回復特性の回路図
Vf-If特性の特性
C-V特性
・章「理論(原理)」
式(1)の補足説明として、今回のダイオードのTTの計算例と補足説明(という体の良い訳)を記載
・節「容量特性の電荷式の分担(容量特性式の第一項をダイオードに戻す)」
説明を追加






コメント スパム対応をしたつもり、コメントは残す方向で頑張ってます