東芝製ダイオード1SS387(参考文献1)をもとに、逆方向特性・順方向特性の容量特性を再現しました。25℃で動作します。
順方向・逆方向のVf-If特性の特性を維持しつつ、容量特性も順方向・逆方向の両方を再現できました。
ただし、順方向特性はデータシートに記載がなかったため、参考扱いとなります。また、公開しているパラメータは共通化ができておらずとっちらかっています。
それでも、データシートに記載されている3項目を同時に再現できたことはとても嬉しく思います。
まとめ
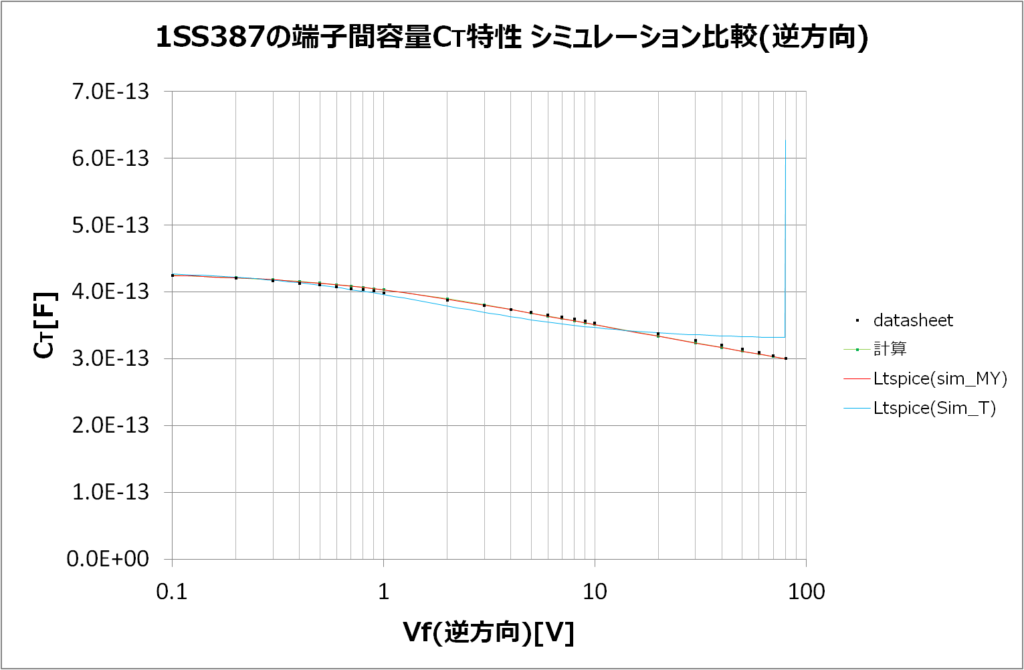
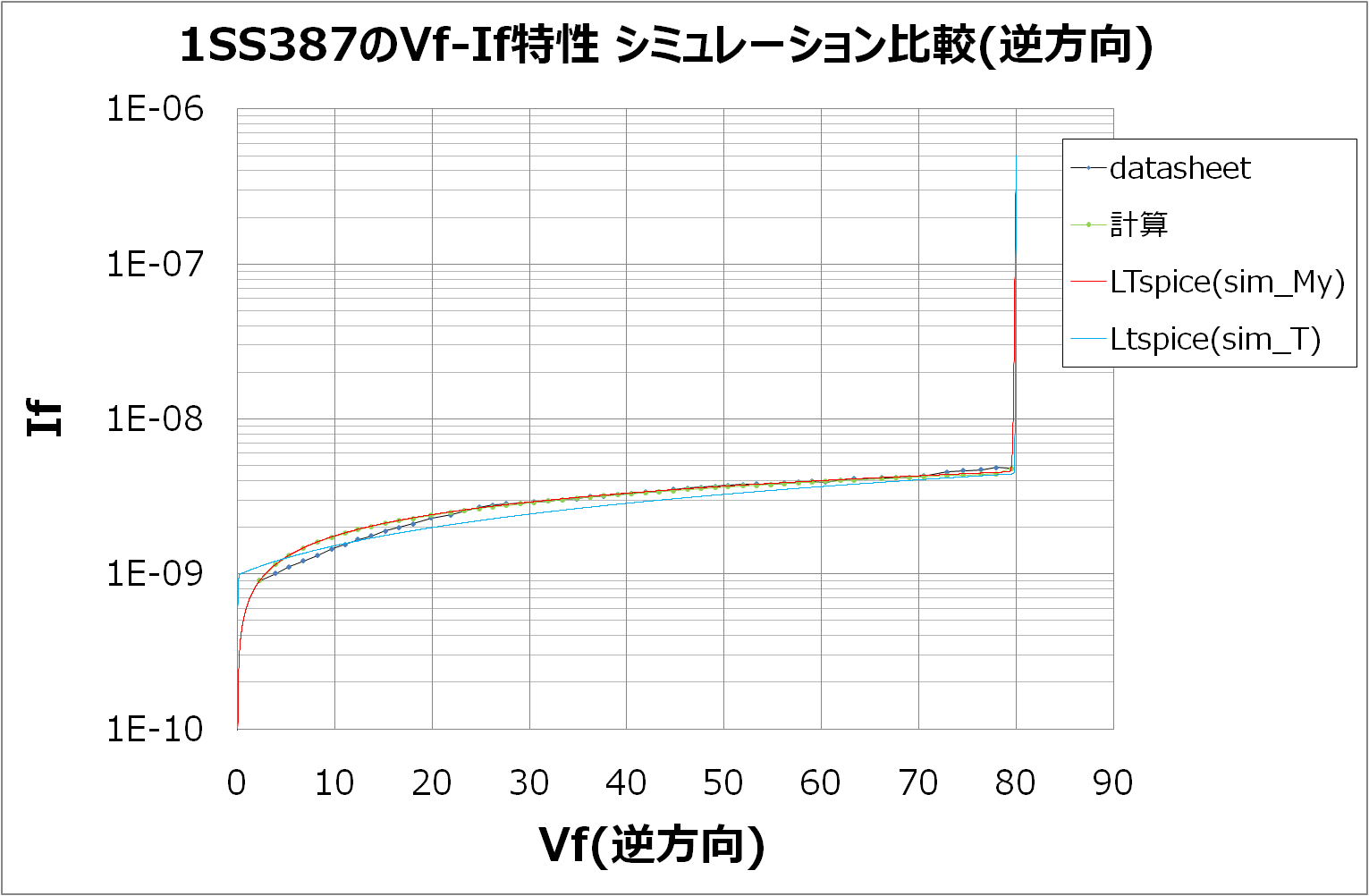
- 逆方向特性はとても精度よく再現できたと思います
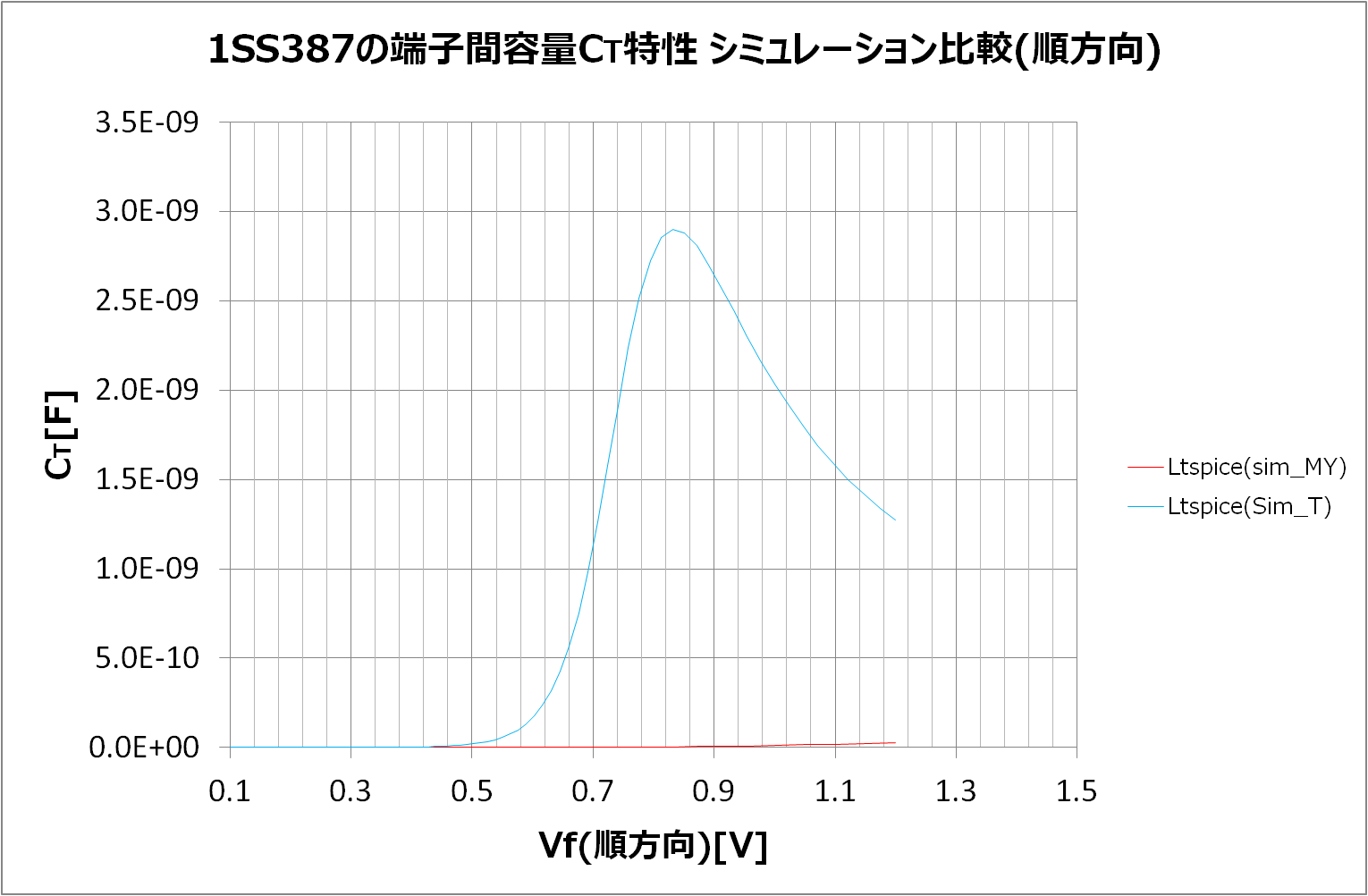
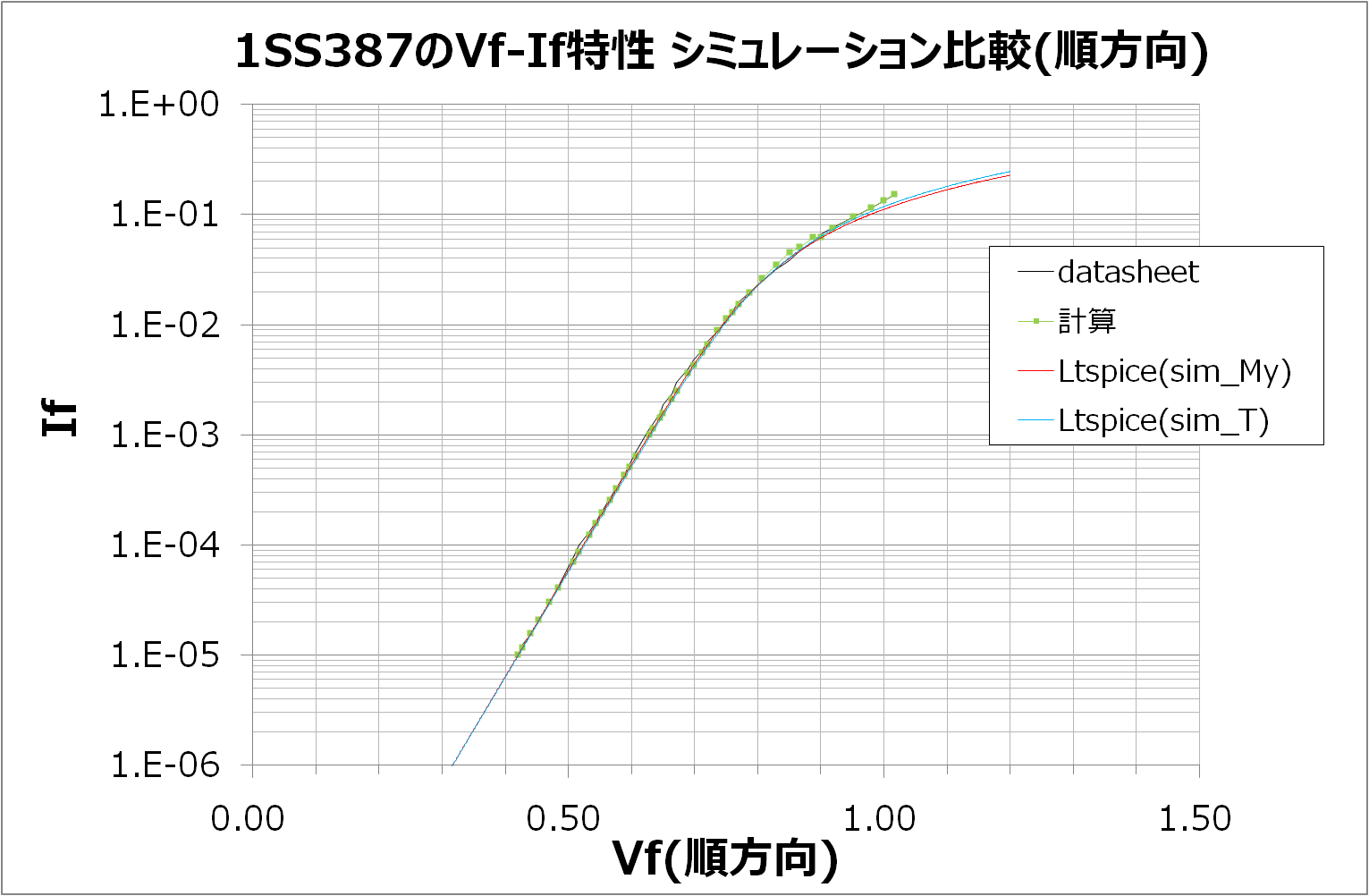
また、Vf-If特性の再結合領域の特性と容量特性が共通のパラメータ"m"を使用している関係上、両方とも精度よく再現することは難しかったのですが、容量特性を電荷Qの独立した式とすることで実現しました - 順方向特性は参考文献2の内容に従った特性として再現できました
はみ出ていたダイオードの容量特性を示す特性式Q=○□の式はこちらです。
わざと改行していません、なので見辛いです。
コピペでペタッとしてください。
Q=if(x<{FC}*{VJ}, {Tt}*{IKF}*{Is}*(2.71828182846)**(({q}*x)/({N}*{k}*(273.15+{T})))-1*{Cjo}*(({VJ}**{m})*(({VJ}-x)**(-1*{m}+1)-{VJ}**(-1*{m}+1)))/(-1*{m}+1), {Tt}*{IKF}*{Is}*(2.71828182846)**(({q}*x)/({N}*{k}*(273.15+{T})))+{Cjo}*(({VJ}/(1-{m}))*(1-(1-{FC})**(1-{m})))+({Cjo}/((1-{FC})**(1+{m})))*(1-{FC}*(1+{m}))*(x-{FC}*{VJ})-{m}*((x**2-({FC}*{VJ})**2)/(2*{VJ})))
ダイオード側のパラメータ
.model 1SS387withoutRs D(
+IKF = 2.34139233921666E-08
+Is = 2.12171244795051E-11
+Rs = 0
+N = 0.86515742147845
+VJ = 1.18162434117476E-05
+m = 0.457215888912848
+Isr = 3.36908794882328E-12
+Nr = 2.08007973691264
+BV = 80
+IBV = 0.0000005
+Nbv = 2.63742401083208
+Ibvl = 1.88400519043853E-20
+Nbvl = 33.6532605476383
+Tt = 0
+Cjo = 0
+FC = 0
+Tnom = 25)
コンデンサ側のパラメータ
.param Tt=4.21063830758098E-07 IKF=2.34139233921666E-08 Is=1.25399258153193E-16 q=1.602176462E-19 N=0.813138907048168 k=1.3806503E-23 T=25 Cjo=4.284042910626E-13 Vj=0.83621131000403 m=0.0778324236418002 FC=0.9
比較として、順方向特性は東芝製ダイオード1SS387のLTspiceモデルをダウンロードして比べてみました(凡例Sim_Tを参照)。
東芝製のモデルはブレークダウンの80Vあたりで容量がグイッと跳ね上がりました。原因は調査していませんので分かっていません
ただ、逆方向・順方向ともに採用している手法がこの記事の方法と比べて違うのではないか、と考えています。逆方向特性は参考文献3(Analog Devices社)にある双曲線正接(tanh)関数の手法を、順方向特性は参考文献2のChawla-Gummelの結果による手法を使っていると考えます。Chawla-Gummelの結果(特性式)は未調査ですのでこの記事では記載していません。
上記により、SPICEでシミュレーションする際はどの手法を使ったか、しっかりと把握しておく必要があります。
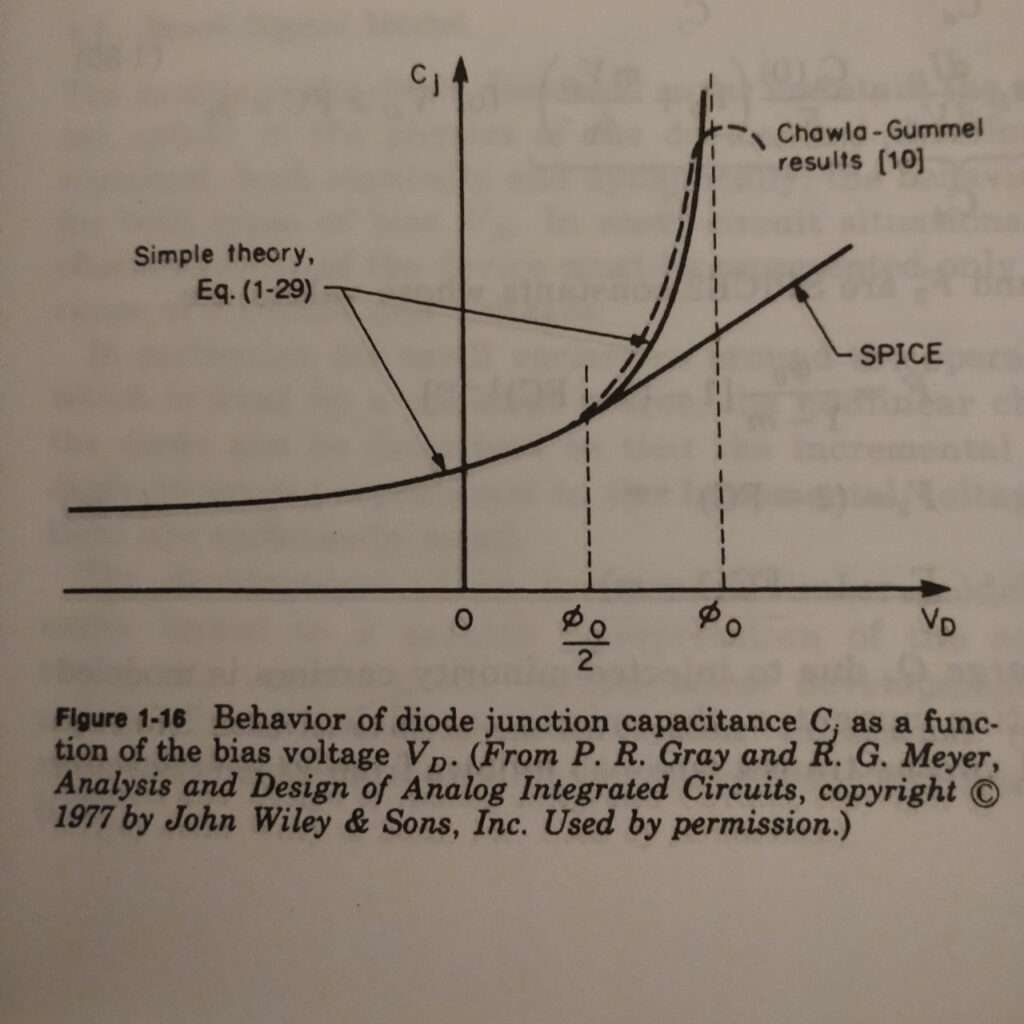
Chawla-Gummelの結果の特性については参考文献2より引用しました。
下図参照ください。
参考文献2:Semiconductor Device Modeling with SPICE SECOND EDITON, GIUSEPPE MASSOBRIO, Tata McGraw Education Private Limited, 1993, Figure1-16 p21
最後に、順方向の容量特性はデータシートの記載がないため、実測してみないことにはわかりません。
ただ、私の家は既にオシロ含め計測器具関係は取っ払ったので調べる術がありません。どなたかFANTASTICな方、実践いただきますと幸いです。
容量特性の再現時の排反:Vf-If特性の逆方向特性の協調が必要
今回の容量特性を再現するときに苦労したことは、ダイオードのVf-If特性と容量特性(順方向・逆方向)の両方を再現することでした。具体的には、Vf-If特性の第二項の式(再結合領域)と容量特性の式で共通のパラメータ"m"を使用していたことでした。
Vf-If特性の第二項の式(再結合領域)の式を次に示します。容量特性の式は次章の式(4)~(7)を参照してください。
\(\displaystyle K_{gen}=\sqrt{\big[(1-\frac{\color{blue}{V_{D_{datasheet}}}-(\color{red}{R_{s}}\color{blue}{I_{D_{datasheet}}})}{\color{red}{VJ}})^2+0.005\big]^\color{red}{m}} \tag{1}\)
\(\displaystyle I_{r}=\color{red}{I_{sr}}\exp\big[\frac{q}{k(273.15+\color{red}{T_{nom}})}*\frac{\color{blue}{V_{D_{datasheet}}}-(\color{red}{R_{s}}\color{blue}{I_{D_{datasheet}}})}{\color{red}{N_{r}}}-1\big] \tag{2}\)
上記の式でパラメータ"m"を使用していることが分かります。そのため、Vf-If特性の逆方向特性を維持しつつ容量特性を再現をすると外れてしまいました。あちらがたてばこちらがたたずの状態になってしまいました。容量特性を再現するときにジャマになってしまいました。
実際に上記式をもとにやってみた結果がこちらです。
Vf-Ifの順方向・逆方向特性をいったん完成させた後、容量特性の再現を試みました。
Vf-Ifの逆方向特性がLTspiceのシミュレーション(容量特性再現の前)から外れていることがわかります。
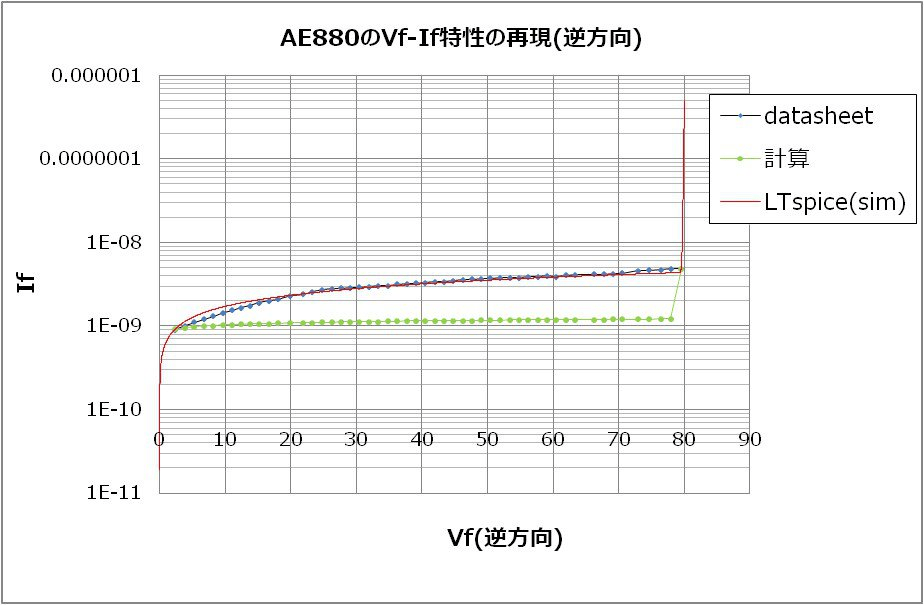
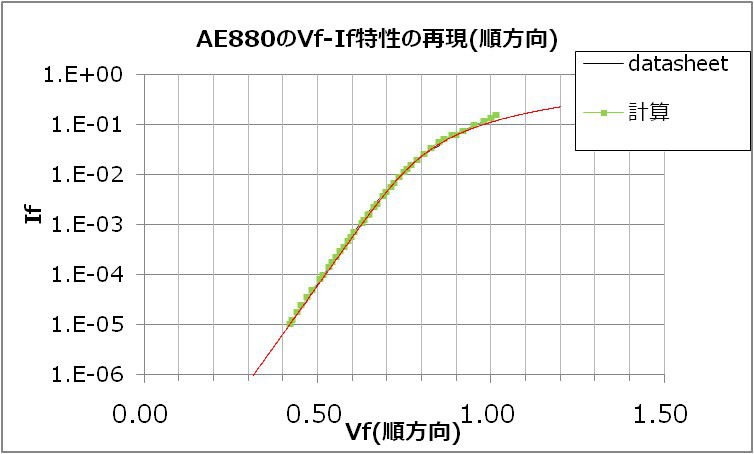
Excelのパラメータ推定時に容量特性をあわせこんだらどうしても逆方向特性があわずでした。
もちろん私のやり方がまずい可能性は十分にあると考ええ、ベストフィットするパラメータの条件があるはずだと色々試行錯誤したのですが、どう頑張ってもできませんでした。ここが今の私の能力の限界です。
そこで、別のアプローチをとることにしました。
具体的には、LTspiceのキャパシタの特性変化式”Q=△□(キャパシタ両端にかかる電圧xの関数)”を利用して、容量特性を独立した形で再現することとしました。次章に記載しています。
Vf-If特性の式についてはこちらにあります(前回の記事)
電荷Q、容量Cの特性式
まずはダイオードの容量特性の関係式をおさえます。
赤文字はExcelソルバーで調整するパラメータです。
青文字はデータシートで確認する値です(定数として扱います)。
今回はパラメータのみの調整でうまくいかなかったため、等価回路モデルになります(個人的には気が進まなかかったのですが致し方なし)。
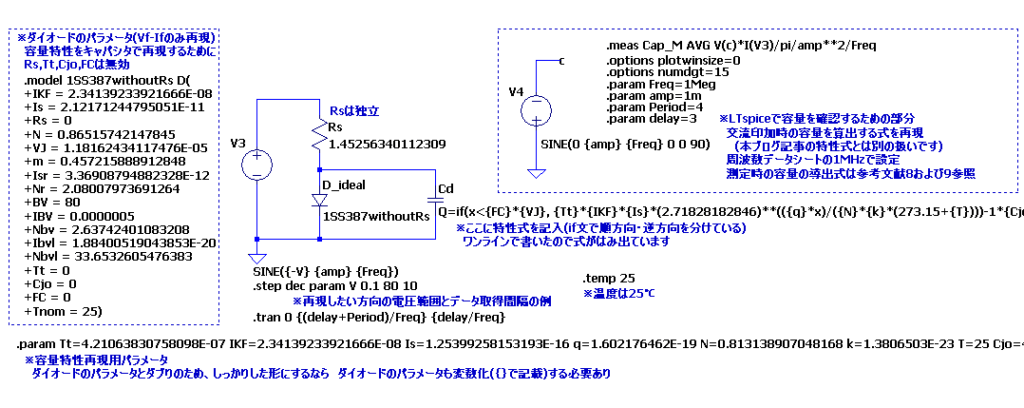
回路図は次の通りです。
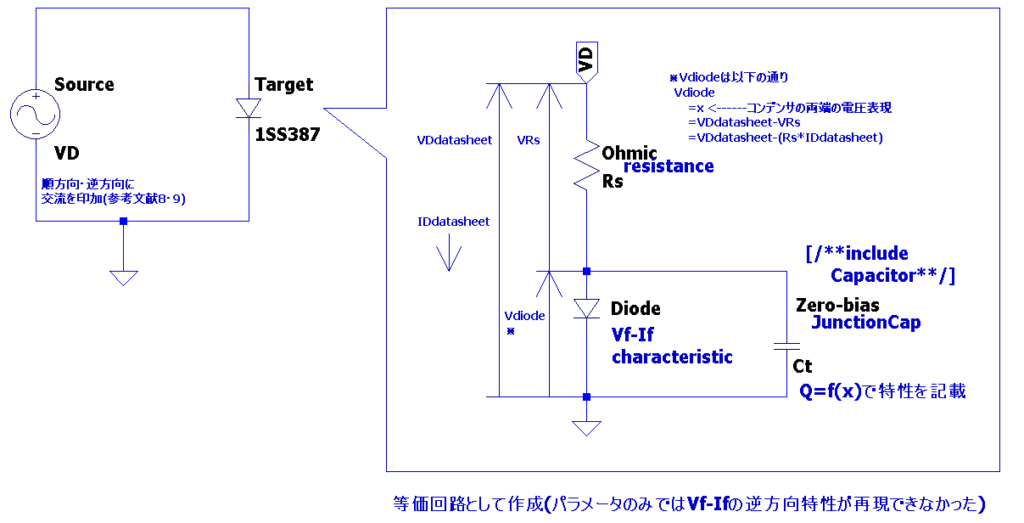
前提:電圧の表現について
LTspice上で指定するコンデンサ両端の電圧\(\displaystyle x\)を必要に応じ表現を分けています。関係式は次の通りです。詳細は後述の章"容量特性算出時の注意点"を参照してください。
\(\displaystyle x=V_{diode}={\color{blue}{V_{D_{datasheet}}}}-\color{red}{Rs}\color{blue}{I_{D_{datasheet}}}\tag{3}\)
x:LTspiceのQの特性式で使用
\(\displaystyle V_{diode}\):xと同じ、数式上でxとすると何を示しているか分からなくなため。
\(\displaystyle \color{blue}{V_{D_{datasheet}}}-\color{red}{Rs}\color{blue}{I_{D_{datasheet}}}\):データシートの値を使用するとき、つまりExcelでパラメータ推定するときに使用
電荷Qの特性式:LTspiceのシミュレーションで使用
参考文献2よりQ、Cは下記の通りです。参考文献2の式では微分や積分の表現を残したままであるため、LTspiceやEXCELの計算で使用できるように展開する必要があります。この記事ではそれらの形に使用できるレベルまで展開しています。ただし、途中計算はのせていません。
一応、参考文献4(Symbolab)や参考文献5(Mathmatica alfa)のサイトで式を入力すればサササーっと積分式を計算してくれます。
(私の学生時代は安くない価格でソフトを買わないとできなかった覚えが...良い時代になったもので多謝)
ただ、私としてはダブルチェックの観点から、念のため手計算でも確認しています。
それでも間違っているやん!と発見した方は是非とも連絡頂きたく。
【逆方向特性】
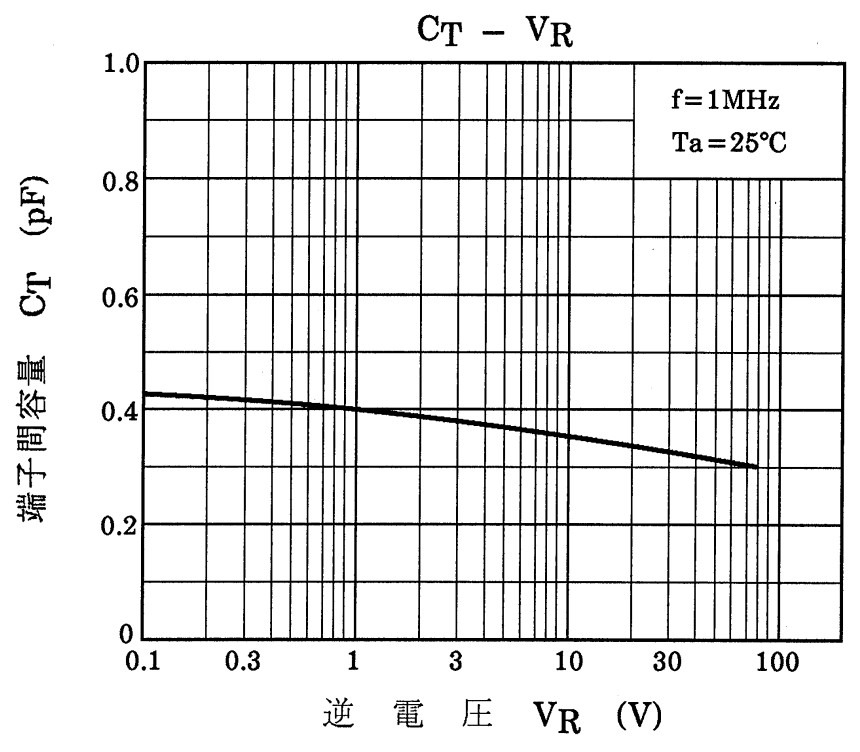
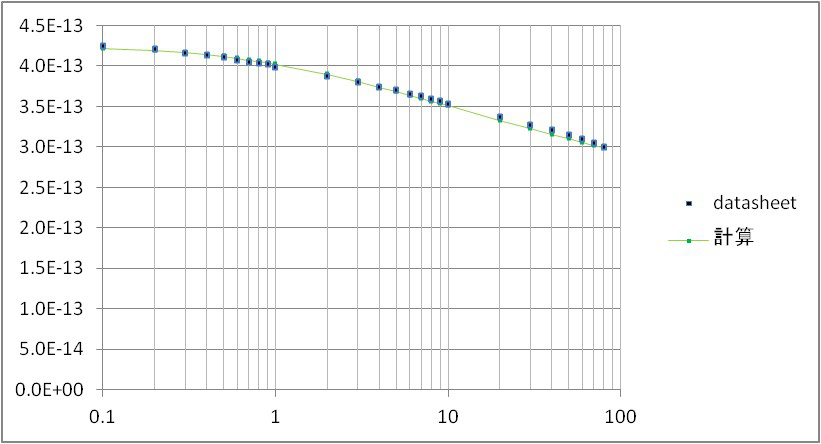
容量の値はデータシートで確認できます。
\(\displaystyle Q_{D}=\color{red}{\tau_{D}}K_{hil}I_{D}+\color{red}{C_{j0}} \int_0^{V_{diode}} (1-\frac{V}{\color{red}{VJ}})^{-\color{red}{m}} dV \ \quad for \quad V_{diode} < \color{red}{FC}*\color{red}{VJ} \tag{4}\)
\(\displaystyle Q_{D}=\color{red}{\tau_{D}}K_{hil}I_{D}-\color{red}{C_{j0}} \frac{\color{red}{VJ}^\color{red}{m}(\color{red}{VJ}-V_{diode})^{-\color{red}{m}+1}}{-\color{red}{m}+1} \quad for \quad V_{diode} < \color{red}{FC}*\color{red}{VJ} \tag{5}\)
[2023/7/30]申し訳ありません、式(5)第二項の符号が誤っていたので修正しました。
("+"を"-"に変更)
【順方向特性】
この特性はデータシートに無い場合がほとんどと見受けられます。1SS387のデータシートにもありませんでした。その場合は参考程度の再現となります。
\(\displaystyle Q_{D}=\color{red}{\tau_{D}}K_{hil}I_{D}+\color{red}{C_{j0}}F1+\frac{\color{red}{C_{j0}}}{F_{2}} \int_{\color{red}{FC}*\color{red}{VJ}}^{V_{diode}} \big(F_{3}+\frac{\color{red}{m}V}{\color{red}{VJ}}\big) dV \ \quad for \quad V_{diode} >= \color{red}{FC}*\color{red}{VJ} \tag{6}\)
\(\displaystyle Q_{D}=\color{red}{\tau_{D}}K_{hil}I_{D}+\color{red}{C_{j0}}F1+\frac{\color{red}{C_{j0}}}{F_{2}} \big(F_{3}(V_{diode}-\color{red}{FC*VJ})+\frac{\color{red}{m}(V_{diode}^2-(\color{red}{FC*VJ})^2)}{2\color{red}{VJ}}\big)\ \quad for \quad V_{diode} >= \color{red}{FC}*\color{red}{VJ} \tag{7}\)
\(\displaystyle K_{hil}=\sqrt{\frac{1}{1+\frac{I_{f}}{\color{red}{I_{KF}}}}} \tag{8}\)
\(\displaystyle I_{D}=\color{red}{I_{S}}\exp\big[\frac{qV_{diode}}{\color{red}{N}k(273.15+\color{red}{T_{nom}})}\big] \tag{9}\)
\(\displaystyle F_{1}=\frac{\color{red}{VJ}}{1-\color{red}{m}}[1-(1-\color{red}{FC})^{1-\color{red}{m}}] \tag{10}\)
\(\displaystyle F_{2}=(1-\color{red}{FC})^{1+\color{red}{m}} \tag{11}\)
\(\displaystyle F_{3}=1-\color{red}{FC}(1+\color{red}{m}) \tag{12}\)
容量C:パラメータの推定(Excelソルバ)で使用
電荷Qの特性式を電圧Vで微分したものがCの式になります。
これはコンデンサの電荷,容量,電圧の関係Q=CVから両辺をVで微分することで算出しています。そのため、式(4)と式(6)の両辺をそれぞれ\(\displaystyle dV\)で微分します。
逆方向特性:式(4)より
\(\displaystyle \frac{dQ_{D}}{dV} = C_{D}=\color{red}{\tau_{D}}G_{D}+\color{red}{C_{j0}}(1-\frac{\color{blue}{V_{D_{datasheet}}}-\color{red}{Rs}\color{blue}{I_{D_{datasheet}}}}{\color{red}{VJ}})^{-\color{red}{m}} \quad for \quad \color{blue}{V_{D_{datasheet}}} < \color{red}{FC}*\color{red}{VJ} \tag{13} \)
順方向特性:式(6)より
\(\displaystyle \frac{dQ_{D}}{dV} = C_{D}=\color{red}{\tau_{D}}G_{D}+\frac{\color{red}{C_{j0}}}{F_{2}}(F_{3}+\frac{\color{red}{m}(\color{blue}{V_{D_{datasheet}}}-\color{red}{Rs}\color{blue}{I_{D_{datasheet}}})}{\color{red}{VJ}}) \quad for \quad \color{blue}{V_{D_{datasheet}}} >= \color{red}{FC}*\color{red}{VJ} \tag{14} \)
\(\displaystyle G_{D}=\frac{dI_{D}}{dV}=\color{red}{I_{S}}\frac{q}{\color{red}{N}k(273.15+\color{red}{T_{nom}})}\exp\big[\frac{q(\color{blue}{V_{D_{datasheet}}}-\color{red}{Rs}\color{blue}{I_{D_{datasheet}}})}{\color{red}{N}k(273.15+\color{red}{T_{nom}})}\big] \tag{15}\)
【パラメータの説明表】
| パラメータ | 内容 | 単位 | default | 補足 |
|---|---|---|---|---|
| Ikf | High-injection knee current. | A | Infin. | |
| Is | saturation current | A | 1e-14 | |
| Rs | Ohmic resistance | Ω | 0.0 | |
| N | Emission coefficient | - | 1.0 | |
| Vj | Junction potential | V | 1.0 | |
| M | Grading coefficient | - | 0.5 | |
| Isr | Recombination current parameter | A | 0.0 | |
| Nr | Isr emission coeff. ※Nrは2以上:参考文献(3)より理論上はNr=2.0(デフォルト値) | - | 2.0 | |
| Ibv | Current at breakdown voltage ※データシートの値を入力 | A | 1e-10 | Vf-If特性 再現でのみ使用 (本記事なし) |
| nbv | Reverse breakdown emission coefficient | - | 1.0 | ↑ |
| Ibvl | Low-level reverse breakdown knee current | A | 0.0 | ↑ |
| nbvl | Low-level reverse breakdown emission coefficient | - | 1.0 | ↑ |
| BV | Reverse breakdown voltage ※データシートの値を入力 | V | Infin. | ↑ |
| Tnom | Parameter measurement temp. | °C | 27 | |
| Tt | Transit-time | sec | 0.0 | 容量特性用 (本記事で使用) |
| Cjo | Zero-bias junction cap. | F | 0.0 | ↑ |
| FC | Coeff. for forward-bias depletion capacitance formula | - | 0.5 | ↑ |
容量パラメータの導出手順
①メーカーのデータシートをダウンロード
②容量特性のグラフから値を抽出
1)参考文献6(WebPlotDigitizer)のサイトを利用
2)使用方法は参考文献7を参照
②ダイオードのVf-If特性を再現(Vf-If特性のパラメータを推定)。Vf-If特性は前回の記事参照
③容量特性を再現(この記事の内容)、章"電荷Q、Cの換算式"のCの式を使います
Excelソルバであわせこんでいきます。
注意点としては、②の特性パラメータが出来上がった後で、かつ容量計算用の別シートにわけて、容量特性のパラメータのみをExcelソルバの対象にしてパラメータ推定を実施します。
やっていること自体はVf-If特性の再現の時と全く同じです。特性式が異なるのみです。
作業時のコツは前回の記事、章”作業手順”と"Excelソルバで作業するときのコツ"を参照してください。
1)データシートの逆方向特性を優先して再現(FC以外のパラメータを決定)
2)順方向特性を再現(FCの決定,ただしデータシートの特性がない場合は参考程度)
④LTspiceでコンデンサの容量入力箇所に電荷Qの式でコンデンサ式(6)と(7)を入力
⑤振幅1mV、周波数をデータシートの値(今回は1MHz)に設定してシミュレーション
具体的な設定シミュレーション方法は三共社様の参考文献8と参考文献9を参照:どちらもpdf直リンク
Vf-If特性の式の再現記事リンク
容量特性算出時の注意点
下記により、Excelでパラメータの算出をする際に誤った電圧の式を使用しないよう、注意が必要です。
LTspiceのダイオードの容量特性は章"電荷Q、容量Cの特性式"にあった電荷式QD=f(\(\displaystyle x\))で表現します。\(\displaystyle x\)はコンデンサの両端の電圧であり、LTspiceでも数式で定義するときは\(\displaystyle x\)を用いて表します。そのため、LTspice上では下記の式にある\(\displaystyle V_{diode}\)はそのまま\(\displaystyle x\)に置き換わります。
式(3)の再掲ですが、LTspice上で指定するコンデンサ両端の電圧\(\displaystyle x\)の別表現は次の通りです。
\(\displaystyle x=V_{diode}={\color{blue}{V_{D_{datasheet}}}}-\color{red}{Rs}\color{blue}{I_{D_{datasheet}}}\tag{3}\)
x:LTspiceのQの特性式で使用
\(\displaystyle V_{diode}\):\(\displaystyle x\)と同じ、式上でかかる電圧の場所を明確にするための表現
\(\displaystyle \color{blue}{V_{D_{datasheet}}}-\color{red}{Rs}\color{blue}{I_{D_{datasheet}}}\):Excelのパラメータ推定で使用
Qの換算式は、電圧項が理想ダイオードの電圧であることです。LTspiceにはコンデンサの両端電圧を表現する変数\(\displaystyle x\)があります。この\(\displaystyle x\)をLTspiceで表記すれば電圧を表現できます。そのため、先ほどの章で示した式Qは積分範囲がVdatasheetではなく、\(\displaystyle x\):コンデンサの両端電圧(=\(\displaystyle V_{diode}\))にかわっています。
理想ダイオードと容量成分のコンデンサは並列につながっているため、ダイオードの両端の電位差はそのままコンデンサにかかる電圧になります。
一方で、Excel上でパラメータを推定するためのCの式ではデータシートに表記されている電圧(ダイオードのリード線から印加する電圧)であるため、理想ダイオード部分にかかる電圧に変換する必要があります。そのために\(\displaystyle \color{blue}{V_{D_{datasheet}}}-\color{red}{Rs}\color{blue}{I_{D_{datasheet}}}\)の式で理想ダイオードにかかる電圧を表現しています。
参考文献
- 1SS387(2022), 東芝デバイス&ストレージ株式会社
https://toshiba.semicon-storage.com/jp/semiconductor/product/diodes/detail.1SS387.html - Semiconductor Device Modeling with SPICE SECOND EDITON, GIUSEPPE MASSOBRIO, Tata McGraw Education Private Limited, 1993
- コンデンサのDCバイアス特性を盛り込んで、LTspiceシミュレーションを実施する, Reiner Bidenbach, Analog Devices, Inc.
https://www.analog.com/jp/analog-dialogue/raqs/raq-issue-192.html - Symbolab
https://www.symbolab.com/ - Wolfram alfa
https://ja.wolframalpha.com/ - WebPlotDigitizer, Ankit Rohatgi, 2010-2022
https://automeris.io/WebPlotDigitizer/ - ブラウザで画像化されたグラフからデータを抽出できるツールWebPlotDigitizerを使ってみる, @atsaki, Qiita
https://qiita.com/atsaki/items/778d3d5d3afd27b58631 - コンデンサの値を動的に可変できるQ=CX 表現, 株式会社三共社, Technical Information LTspice TIPS, 株式会社三共社, 渋谷道雄, 2020年4月15日
https://www.sankyosha.co.jp/engineer_doc/pdf/2004-1_Q_CX_Expression.pdf - 半導体素子の(逆バイアス時の)接合容量をシミュレーションで知る方法, Technical Information LTspice TIPS, 株式会社三共社, 渋谷道雄, 2020年3月15日
https://www.sankyosha.co.jp/engineer_doc/pdf/2003-4_Capometer.pdf
変更履歴
記事UP
・工事中の内容を作成
・ダイオードの等価回路図に使用していた引用を削除(ここに残します)
このリンクの図4が近いです。
引用:独立行政法人高齢・障害・求職者雇用支援機構 職業能力開発総合大学校 基盤整備センター
・広告(Google Adsence)を除外
・誤字脱字、その他フォントなど体裁関係を修正
・参考文献の画像を引用タグの中に入れた
・冒頭部
都度更新する旨の補足を削除
まとめにLTspiceで使用するコンデンサの特性式を追加
1SS387のパラメータを追加
・体裁関係修正
・サムネイル追加
・冒頭部
「また、公開しているパラメータは共通化ができておらずとっちらかっています。」を追加
・章「容量パラメータの導出手順」で"注意点としては、②の特性パラメータが出来上がった後で、かつ容量計算用の別シートにわけて、容量特性のパラメータのみをExcelソルバの対象にしてパラメータ推定を実施します。"を追加。
・全体の誤字脱字修正
・冒頭部
”結果と説明”のLTspiceの回路図の画像を差し替え(誤記あり)
誤り(変更前)の画像の通りに回路図を組むと、
.meas にてCap_Mがエラーになり計算されませんでした(未定義の変数呼び出しのため)
誤:Frec
正:Freq
・まとめ部
LTspiceに貼り付ける用のQ=○□の式で記号"*"が抜けていた内容を修正
・式(5)
式の誤り修正(第二項の”+”を”-”に変更)




コメント スパム対応をしたつもり、コメントは残す方向で頑張ってます